小さなピークと大きなピークを交互に繰り返す関数

小さなピークと大きなピーク

　微分積分ではおなじみのカテナリー曲線
　
\[y=\frac{a(e^{x/a}+e^{-x/a})}{2}\]
において $a=1$ とし、$\sin x$ を入れ子にした合成関数
　
\[f(x)=\frac{1}{2}\{\exp(\sin x)+\exp(-\sin x)\}\tag{1}\]
を考えてみます。この関数は周期に関して面白い性質があります。合成関数の微分公式を使って導関数を求めると、
　
\[\begin{align*}f'(x)&=\frac{1}{2}\{\cos x\exp(\sin x)-\cos x\exp(-\sin x)\}\\[6pt]
&=\frac{1}{2}\{\exp(\sin x)-\exp(-\sin x)\}\cos x\end{align*}\]
　$y’=0$ とおくと、極値を求める方程式
　
\[\begin{align*}&\cos x=0&\quad (2)\\[6pt]
&\exp(2\sin x)=0&\quad (3)\end{align*}\]
が得られます。(3) から $\sin x=0$ なので、$y=f(x)$ は $\sin x=0$ または $\cos x=0$ となる点、すなわち
　
\[x=\cdots,\ -\pi,\ -\frac{\pi}{2},\ 0,\ \frac{\pi}{2},\ \pi\, \cdots\]
で極値をとることになります。実際に Excel でグラフを描いてみると、次のようになります。

　

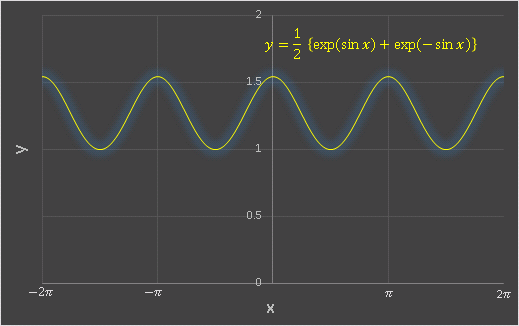
　$x=n\pi$ で極大値、$x=1/2+n\pi\ (n=0,\ \pm 1,\ \pm 2\, ……)$ で極小値となっています 。(3) を一般化して、
　
\[p(x)=\frac{1}{2}\left\{\exp(q(x))+\exp(-q(x))\right\}\]
という合成関数を定義して、色々な $q(x)$ を選んでグラフを Excel で描いてみます。$q(x)=\cos 2x+\sin x$ としてみると ……

　

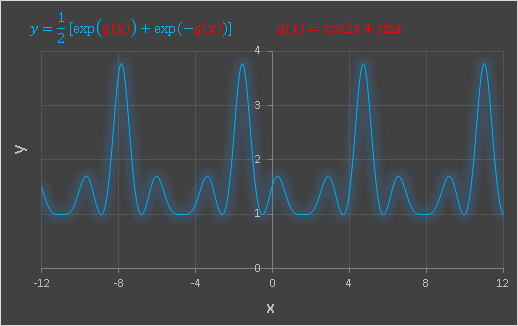
　小さなピーク が 2 回続いたあとに、大きなピーク が 1 回現れるという周期をもつ関数です。次は
　
\[q(x)=\frac{\cos x}{x^2+1}\]
としてみます。

　

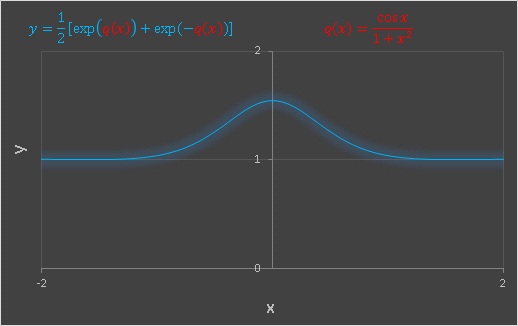
　原点にピークを１つだけもつグラフです。これを少し変形して
　
\[q(x)=\frac{x\cos x}{x^2+1}\]
としてみると ……

　

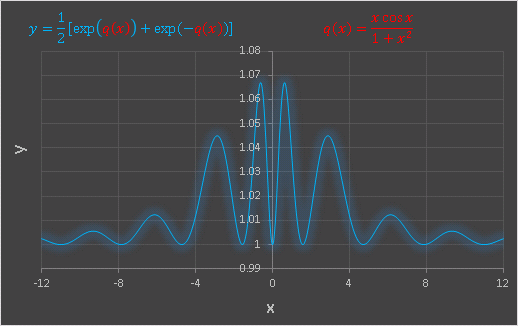
　原点付近で大きく振動し、両端に向かって減衰していくグラフです。
　$q(x)$ の $\cos x$ を $\sin x$ に変えて
　
\[q(x)=\frac{x\sin x}{x^2+1}\]
としてみると、次のようなグラフが描かれます。

　

ChatGPTに複数のピークをもつ関数について尋ねてみました

　ChatGPT に「複数のピークをもつ数学関数を教えてください」と尋ねると、以下のような答えが返ってきました（あくまで人工知能の答えなので真偽については保証できません。）。

[ChatGPT] 以下に、複数のピークを持つ数学関数をいくつか紹介します。

コーシー分布：コーシー分布は、中央値がある位置でピークを持ち、左右に裾野が広がる関数であり、複数のピークを持つことがあります。

三角関数の和：三角関数の和を取ることで、複数のピークを持つ関数を作ることができます。例えば、f(x) = sin(x) + sin(2x) + sin(3x)は、3つのピークを持つ関数であり、ピークはx=kπ/2 (kは整数)のときに現れます。

多項式関数：高次の多項式関数は、複数のピークを持つことがあります。例えば、f(x) = x^4 – 2x^3 – x^2 + 2x + 1は、4つのピークを持つ関数であり、ピークはそれぞれx=-1.3、x=-0.3、x=1、x=1.3のときに現れます。

ガウス関数の和：複数のガウス関数の和を取ることで、複数のピークを持つ関数を作ることができます。例えば、f(x) = exp(-(x-1)^2) + exp(-(x+1)^2)は、2つのピークを持つ関数であり、ピークはそれぞれx=1、x=-1のときに現れます。

　これらの関数は、複数のピークを持つことで異なる特徴を持ち、多くの場合、科学や工学、経済学などの応用分野で使用されます。