年齢算とは、ある時点での2人の人物の年齢をもとに、年上の人物の年齢が年下の人物の年齢の整数倍になるのはいつかというようなことを求める問題です(複雑な問題になると人数が増えたりします)。解法パターンを覚えてしまえば基本問題は解けるようになりますが、もう少し掘り下げて年齢算のメカニズムを知っておくと複雑な応用問題にも対処できるようになります。
年齢算の基本問題
まずは年齢算の基本問題を見てみましょう。
【例題01】ゆかりさんは現在 38 歳で、息子の正太郎君は 8 歳です。
(1) ゆかりさんの年齢が正太郎君の年齢の 3 倍になるのは何年後ですか。
(2) ゆかりさんの年齢が正太郎君の年齢の 6 倍だったのは何年前ですか。
【解答】(1) 年齢算を解くコツは、いったん現在の年齢を忘れて、2人の年齢差だけに着目することです。何年後であろうと、何年前であろうと、ゆかりさんと正太郎君の年齢差は決して変わりません(当たり前です)。そこで、ゆかりさんの年齢が正太郎君の年齢の 3 倍になっているという状況を図に描いてみます。
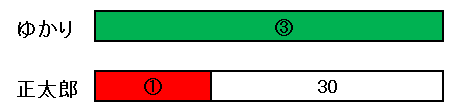
〇で囲っている数字は比率です。
ゆかりさんが ③ に対して、正太郎君は ① です。
白い部分が2人の年齢差 30 歳を表しています。
この 30 に相当する比率は ③ - ① = ② ですね。
つまり ① に相当する数は 30 ÷ 2 = 15 ということになります。
よって正太郎君が 15 歳、ゆかりさんが 45 歳のときに年齢は 3 倍になるので、それは今から 15 – 8 = 7 年後ということになります。
(2) 同じように図を描いてみます。

今度は 30 に相当する比率は ⑥ – ① = ⑤ ですね。
① にあたる数字は 30 ÷ 5 = 6 です。
よって正太郎君が 6 歳、ゆかりさんが 36 歳のときに年齢は 6 倍になり、それは今から 8 – 6 = 2 年前ということになります。
年齢算の仕組み
さきほどの【例題01】を使って年齢算の仕組みを調べてみましょう。まずはゆかりさんが正太郎君を産んだとき(ゆかりさんが 30 歳、正太郎君が 0 歳)から1年ごとの経過を見てみます。
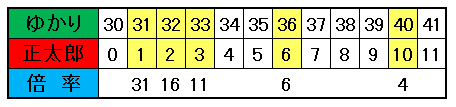
黄色く塗ってある部分が年齢が整数倍になる組合せです。一番下にその倍率が載っていますが、その倍率は
31, 16, 11, 6, 4, …
というように年数が経過するごとに小さくなっていきます。また、年齢が整数倍になる周期は一見して不規則に思えますが、正太郎君の年齢に着目すると
1, 2, 3, 6, 10, …
となっていて「年齢差 30 の約数になっているのではないか?」と推測できます。残り全ての数字を並べて調べるのは大変なので、もう少し別のアプローチでこの推測の正しさを確認してみましょう。そこで先程と同じような図を描いてみます。
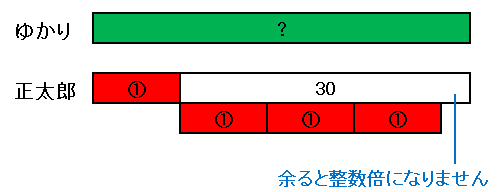
今回は年齢の倍数は定めていませんが、どのような状況であっても年齢が整数倍になるためには、①に当たる数は 30 の約数になっていなければならないことがわかります(つまり図にあるように、①を整数個並べてきっちり 30 になっている必要があるということです)。よって正太郎君の年齢は
1, 2, 3, 6, 10, 15, 30
のいずれかであり、(正太郎君の年齢、ゆかりさんの年齢) という組合せを並べてみると、
(1, 31), (2, 32), (3, 33), (6, 36), (10, 40), (15, 45), (30, 60)
と有限個数になっています。正太郎君が 30 歳を超えると、あとは2人がどれだけ長生きしても整数倍になることはありません。
同じことを方程式を使って確認してみましょう。
年齢算は一種の整数問題となっています。
正太郎君の年齢を m, ゆかりさんの年齢を m + 30 とおくと
m + 30 = km
という方程式を立てられます(k は自然数)。少し変形すると
m = 30/(k – 1)
となるので、 m が整数であるためには
k – 1 = 1, 2, 3, 5, 6, 10, 15, 30
のいずれかでなければならず、そのとき正太郎君の年齢 m は
m = 30, 15, 10, 6, 5, 3, 2, 1
となります。よって、(正太郎君の年齢、ゆかりさんの年齢) の組合せは
(1, 31), (2, 32), (3, 33), (6, 36), (10, 40), (15, 45), (30, 60)
となります。
年齢算の応用問題
もう少し難しい問題に挑戦してみましょう。
【例題02】ゆかりさんは現在 35 歳で、息子の正太郎君は 5 歳、娘の真奈ちゃんは 4 歳です。ゆかりさんの年齢と真奈ちゃんの年齢の和が、正太郎君の年齢の 3 倍になるのは何年後ですか?
【解答】ゆかりさんと真奈ちゃんの年齢の和が 1 年ごとに 2 ずつ増えていくことに注意します。正太郎君の年齢は 1 年ごとに 1 ずつ増えるので、このままでは比較できません。そこで正太郎君の年齢を 2 倍にして 1 年ごとの年齢増加を 2 に揃えます。そして「ゆかりさんと真奈ちゃんの年齢の和」から「正太郎君の年齢の 2 倍」を差し引くと
35 + 4 – 5 = 29
となります。この状況を図示すると次のようになります。
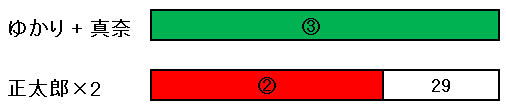
正太郎君の年齢の比率も 2 倍の②となっていることに注意してください。③から②を引いた①が 29 に相当するので、正太郎君が 29 歳のときに問題の条件を満たします。よって 29 – 5 = 24 年後が答えです。

エクセルや数学に関するコメントをお寄せください