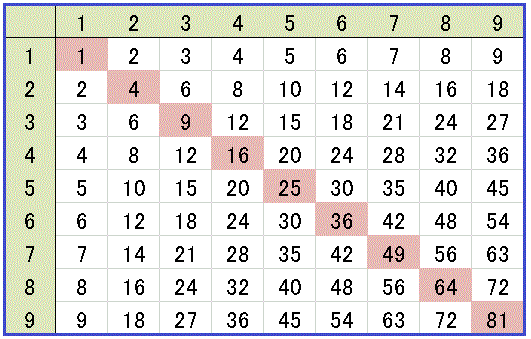
上図は「九九」の数表です。懐かしいですね。昔は 7 × 8 = 56 など、いわゆる 4 桁の数字をずらずらとたくさん覚えたのですから、子供の記憶力とはすごいものです。大人になると 2 つか 3 つのパスワード覚えるだけで四苦八苦しますからね。
実はこの「九九」の数表には数学の大切な仕組みが色々と隠されています。
しばらくは、この数表に隠されているものを色々と探してみましょう。
さて数学には、その問題によって「数」を「数量」のイメージで捉えるときと、「大きさ」のイメージによってアプローチするときがあります。「数量」は方程式を解く場合などで、「大きさ」は図形問題を扱う場合に主に用います。もちろんどちらも「数」であることに変わりないので、「数量」感覚でダメなら「大きさ(図形)」感覚に変えてアプローチし直したり、またその逆をしたりと、この2種のイメージ間を行ったり来たりします。
「九九」を面積でイメージします
「九九」の数表は明らかに「数量」感覚ですが、これを図形的なイメージに変換すると下の図のようになります。
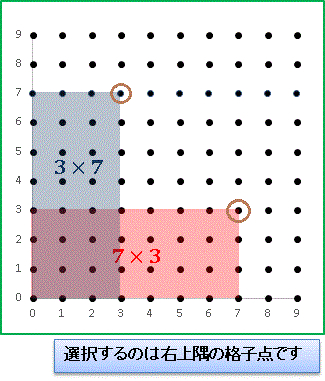
0 × 0 を含めて縦横に格子点が全部で 100 個打たれています。
図の赤い長方形を見てください。横に 7 つめ、そこから数えて縦に 3 つめの点を選べば、それは 7 × 3 に対応しています。その大きさは
赤い部分の面積 = 横 × 縦 = 7 × 3 = 21
というように面積でイメージすることができます。
「左下隅を固定して右上隅にある格子点を選んで長方形を作る」というルールに従えば、図中のあらゆる格子点は 0 の列を除いて必ず「九九」に対応しています。「九九」のあれこれを実際にいくつか試して確認してください。
「九九」には同じ掛け算が含まれています
「九九」の数表には、ある掛け算に対して、順番を変えるだけの掛け算が必ず対で存在していますね。
7 × 3 = 21, 3 × 7 = 21
などです。これを先ほどの図形版で見ると、赤い長方形と青い長方形が対応しています。同じ形と大きさで置いてある向きが異なるだけですね。このように掛け算は順序を変えても同じ結果が得られます。「当たり前でしょー」と思われるかもしれませんが、実は数学の世界には「順番を変えると異なった結果になってしまう」操作も存在しています。それはずっと先で扱いますが、「操作の順序」というのはとても大切な概念であることを頭の片隅に残しておいてください。
0 の列にも大切な意味があります
一番下(縦の長さ0)や一番左(横の長さ0)に並ぶ格子点を選ぶと長方形を作ることはできません。潰れてしまって線分になり「面積は 0 」になってしまいます。
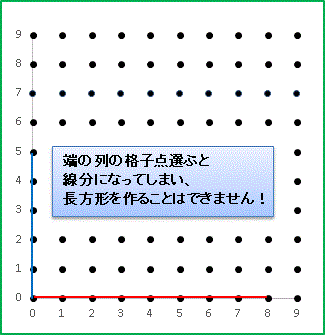
この図には「0 にどのような数を掛けても 0 である」という 0 の性質が自然な形で表れていますね。
九九の数表を拡大します
少し前に流行ったインド式数学の本などには、九九の数表を拡大して 19 × 19 まで覚えた方が良いと書いてありました。いえ、実のところ私も「そうなのかー!」とあっさり流行に乗っかって必死に覚えたりもしたのですが、冷静に考えると平方数を覚えたほうが有用だと思うようになりました。平方数というのは同じ数を掛け算した数字です。「九九」の数表では赤く網掛けされた数字ですね。そして「九九」図形版では …
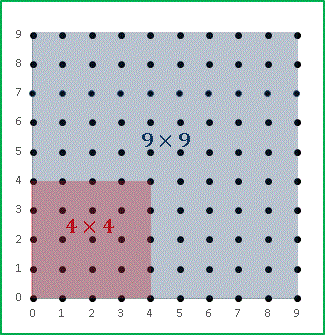
このように正方形となっています。「平方数」=「正方形」というイメージを頭の中に定着させてください。中学生になると「42 = 16」、「92 = 81」のように恰好良く書いたりしますね。この平方数をもっとたくさん、たとえば、「13 × 13 = 169」、「25 × 25 = 625」などを覚えると、次のような計算で役立ちます:
13 × 14
14 = 13 + 1 ですから、上の式を書き直すと、
13 × (13 + 1) = 169 + 13 = 182
のように、13 × 13 を覚えていれば、ちょっと足し算すると平方数に近い計算ができます。また、「15 × 17」のように、平方数から2つ数がずれていても、15 × 15 = 225 を知っていれば何とかなります:
15 × 17 = 15 × (15 + 2) = 225 + 30 = 255
下に 11 × 11 から 30 × 30 までの平方数を載せておきます。今の段階で無理に覚える必要はありませんので、この表を見ながら下の計算問題を解いてみてください。
| 11×11 = 121 | 21×21 = 441 |
| 12×12 = 144 | 22×22 = 484 |
| 13×13 = 169 | 23×23 = 529 |
| 14×14 = 196 | 24×24 = 576 |
| 15×15 = 225 | 25×25 = 625 |
| 16×16 = 256 | 26×26 = 676 |
| 17×17 = 289 | 27×27 = 729 |
| 18×18 = 324 | 28×28 = 784 |
| 19×19 = 361 | 29×29 = 841 |
| 20×20 = 400 | 30×30 = 900 |
【問題01】(1) 11×12 (2) 14×15 (3) 17×19 (4) 25×24 (5) 25×23
難しいと感じたら、無理に暗算しようとせずに紙に書いてゆっくり計算してくださいね。慣れていないうちは、数字が 2 つ以上ずれると暗算はけっこう難しいです。できたら下の解答と照らし合わせてみてください。
【解答】
(1) 11×12 = 11×(11 + 1) = 121 + 11 = 132
(2) 14×15 = 14×(14 + 1) = 196 + 14 = 210
(3) 17×19 = 17×(17 + 2) = 289 + 34 = 323
(4) 25×24 = 25×(25 – 1) = 625 – 25 = 600
(5) 25×23 = 25×(25 – 2) = 625 – 50 = 575
(4) と (5) では ( ) の中を引き算にしています。 23×23 = 529 に比べて 25×25 = 625 という数字のほうがずっと扱いやすいからです。このように、なるべく扱いやすい式を基準に計算するのがコツです。したがって特に頭に入りやすい平方数として、次の式だけでも暗記しておくと便利です。
11×11 = 121、 15×15 = 225、 21×21 = 441、 25×25 = 625
「21×21 = 441 が何で扱いやすいの?」と思われるかもしれませんが、下一桁 1 の数字は、下一桁 0 の数字の次に重宝します。というのは、この下一桁に 1 から 8 まで加えるような計算で繰り上がりが生じないからです。たとえば、
21×23 = 21×(21 + 2) = 441 + 42 = 483
という計算は、どの桁でも繰り上がりがないので暗算しやすいのです。
平方数にはちょっと面白い秘密が隠されています。それは、
【秘密①】平方数を 3 で割った余りは 0 か 1
【秘密②】平方数を 4 で割った余りは 0 か 1
というものです。「ほんとかなー?」と疑問に思ったら、ともかく試してみましょう。先ほどの表から適当な平方数を選んで問題にします。筆算で確認してください。
【問題02】
(1) 17×17 = 289 を 3 で割って商と余りを求めてください。
(2) 17×17 = 289 を 4 で割って商と余りを求めてください。
【問題02の解答】
(1) 17×17 ÷ 3 = 289 ÷ 3 = 96 ・・・ 1
(2) 17×17 ÷ 4 = 289 ÷ 4 = 72 ・・・ 1
ほらね。ちゃんと余りは 1 になってます。
え? 偶然じゃないの? それならもう1つ試してみましょう。
【問題03】
(1) 28×28 = 784 を 3 で割って商と余りを求めてください。
(2) 28×28 = 784 を 4 で割って商と余りを求めてください。
【問題03の解答】
784 ÷ 3 = 261 ・・・ 1
784 ÷ 4 = 196 ・・・ 0
どうです? 3 で割ったら余りは 1 だし、4 で割り切れてます。
ええ!? まだ疑うんですか? そうですね。実は数学ではそういう「疑り深い心」が大切なんです(こう書くと数学やってる人が性格悪いみたいに思われてしまいますけど …)。きちんと全ての平方数にたいして成り立つことを確認しないと本当の「証明」とはいえません。でもその証明法は今の段階ではまだ難しいので、今回のところは「疑わしいけど、まあ一応信じておいてやるか」ぐらいに思っておいてください。
九九の数字を全て足し合わせてみます
九九の表にある数字を全て足し合わせるといくつになるでしょうか。とはいえ、いくらなんでも 1 マスずつ全部足していたら大変です。もう少し上手い計算法がないか考えてみましょう。

とりあえず 1 列目が簡単そうなので書き出してみます。
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9
これぐらいなら順番に足しても大したことはなさそうですが、「もっと怠けて楽ができないかな?」とぎりぎりまで横着を追及するのが数学を上達させるコツです。頑張り屋さんは、もっと面倒くさがりにならないといけません。上の足し算で頭と末尾の数字に注目してください。 1 と 9 ですね。これを足すと 10 です。では次に 2 と 8 を足します。これも 10 となります。こういうペアを作った順に書き直して
(1 + 9) + (2 + 8) + (3 + 7) + (4 + 6) + 5
最後に 5 が余ってしまいましたけど、ペアとなる相手がいないので仕方ありません。上の式は 10 が 4 つと 5 が 1 つですから、
10 × 4 + 5 = 45
と計算できますね。これで 1 列目が計算できました。「よーし。じゃあ 2 列目も同じように計算するぞ」という人は、まだまだ真面目すぎます。可能な限り面倒を避けて横着をする。これが数学の基本姿勢だということをお忘れなく。もう 1 度、九九の表を見てみましょう。
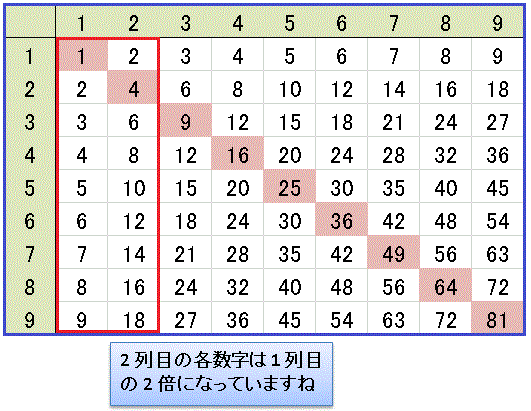
2 列目の各数字は全て、左隣にある 1 列目の数字の 2 倍になっていますね。
ということは、足し合わせた数字も 1 列目の 2 倍になっているはずですから 45 × 2 を計算すればいいのです。「なるほど! それなら次は 3 列目、4 列目を次々と計算して最後に足し合わせれば答えが出るぞ」とか思った人は「面倒くさがり道場」で修業してきてくださいな。全てのマス目の数の和 S を表すと
S = 45 × 1 + 45 × 2 + 45 × 3 + …… + 45 × 9
のように書けるはずです。「…」は「こんな感じで続きますよ」という記号です。数学ではこういう記号も上手く使って労力を惜しみます。上の式は ( ) を使って次のように書くことができますね。
S = 45 × (1 + 2 + 3 + … + 9)
よく見てください。 ( ) は先ほど計算した 1 列目の足し算と同じですから、
S = 45 × 45 = 2025
が答えになります。このように算数や数学では、がむしゃらに計算して答えを出すことではなく、いかに上手く労力を節約して答えに辿り着いたか、という過程がとても大切なのです。

エクセルや数学に関するコメントをお寄せください