【Excel】誕生日が一致する確率を計算します

【EX11】クラスの中に同じ生年月日の人がいる確率は？

ある学校に 30 名からなるクラスがあります。この中に同じ誕生日の生徒が少なくとも 2 名いる確率を Excel で計算してください。ただし、この学年の生徒たちが生まれた年はうるう年ではなかったとします。

【ヒント】「少なくとも 2 人」を裏返すと…？　計算式がわかっても、数式をそのまま Excel に入力すると大変面倒です。

【解答】いきなり 30 人で考えると大変なので、まずは A 君、B 君、C さんの 3 人のうち少なくとも 2 人の誕生日が一致する確率を計算してみます。「少なくとも 2 人の誕生日が一致する」というのは、「全員の誕生日が違っている」ことと裏返しの関係にあります。つまり「少なくとも 2 人の誕生日が一致する確率」は

1 － [全員の誕生日が違っている確率]

ということになります。そこで 3 人のうち 1 人の A 君に注目して、B 君と誕生日が違っている確率を考えます。B 君の誕生日は、365 日から A 君の誕生日である 1 日を差し引いた 364 日のうちのどれかということになります。つまり「 B 君と A 君の誕生日が一致しない確率」は
 \[\frac{364}{365}\]
と計算できます。そして C さんの誕生日は残りの 363 日のうちどれかなので、「全員の誕生日が違っている確率」は
 \[\frac{364\times 363}{365\times 365}\]
となります。よって「少なくとも 2 人の誕生日が一致する確率」は
 \[1-\frac{364\times 363}{365\times 365}\]
と計算できます。これが 30 人になっても同じように考えて、少なくとも 2 人の誕生日が一致する確率は
 \[1-\frac{364\times 363\times 362\cdots}{365\times 365\times 365\cdots}\]
となります（分子と分母で 30 より 1 つ少ない 29 個の数が掛け算されます）。しかし、この数式をそのまま Excel に入力するのは大変ですから、次のような手順で計算します。
 

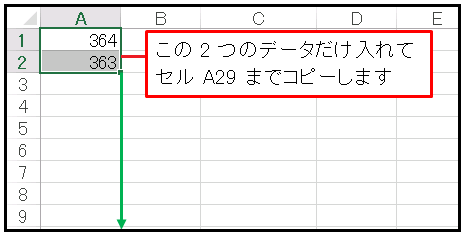
まず上の図にあるように、セル A1 に 364, A2 に 363 という数を入力し、この 2 つのセルを同時に選択した状態で、右下隅をセル A29 までドラッグしてコピーします。「連続データ作成機能」を使ってもいいのですが、この程度のセル数であれば普通にコピーしたほうが速いです。
 

セル A1 から A29 までの数値をまとめて掛け算するために PRODUCT関数を使います。どこかのセルに

1-PRODUCT(A1:A29)/365^29

と入力すれば、0.7063 … という確率が得られます。30 人も集まると、たいていの場合は自分と同じ誕生日の人がいるということですね。

【EX12】10万日後の日付

(1) 2017 年 9 月 24 日から 10 万日後の日付を求めてください。
(2) 2017 年 9 月 24 日から 3000ヶ月後の日付と曜日を「？年？月？日？曜日」の形式で表示させてください。

【ヒント】Excel では 1900 年 1 月 1 日を起点とする日数で日付を処理しています。この数値（日数）のことをシリアル値とよびます。セルに 2017/9/24 と表示されていても、表示形式を [数値] に変えてみると、実は 43002 という数字であることがわかります。つまり日付に対する + 1 という演算は「1 日を加える」ことを意味しています。しかし、日付に月数を加える場合は、ある関数を使う必要があります。日付と曜日を並べて表示させるのは、やや難しいテクニックです。

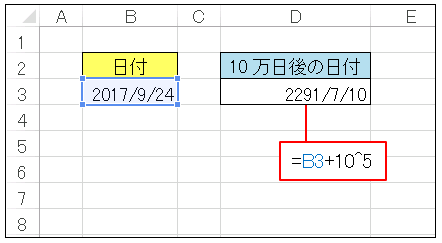
【解答】(1) たとえば、セル B3 に 2017/9/24 のような形式で日付を入れておきます。そして別のセルに

=B3+10^5

と入力すると、「2291/7/10」という日付が表示されます。
 

 
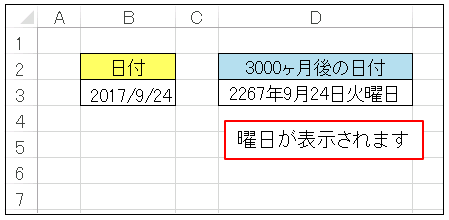
(2) 月数を加えるときには EDATE 関数 を用います。たとえば、セル B3 に「2017/9/24」のような形式で日付を入れてある場合、別のセルに

=EDATE(B3,3000)

と入力すれば、「2267/9/24」と表示されます。
 

 
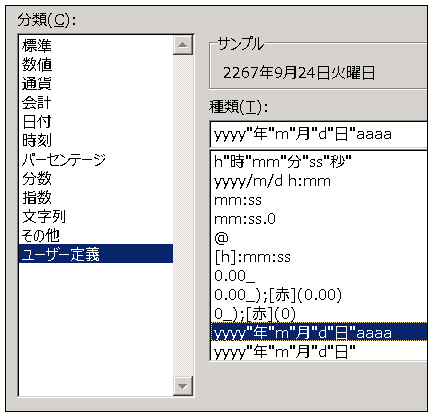
しかし初期設定では曜日までは表示されないので、[セルの書式設定] 画面を開いて [分類] をユーザー定義関数とし

yyyy"年"m"月"d"日"aaaa

のように設定します(aaaa が曜日の表示設定です)。
 

 
すると、「2267年9月24日火曜日」と表示されるので、答えは「火曜日」であることがわかります。