場合の数（樹形図・積の法則・和の法則）

樹形図

1 枚の硬貨を続けて 3 回投げて、少なくとも 2 回表が出るケースは何通りあるでしょうか。「少なくとも 2 回」ということは、「3 回続けて表が出る」というケースも含みます。1 回目は表と裏の 2 通りです。そして、1 回目が表であったときに、2 回目も表となるのは…ということを丁寧に図にしてみると次のようになります。
 

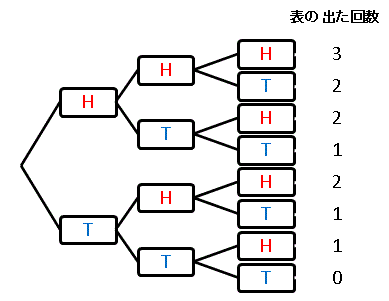
コインの表を H (heads)、 裏を T (tails) という記号表しています。
このような図を樹形図（tree）とよびます。実際に書くのはちょっと大変ですが、書いたあとは数えるだけなので確実に答えを知ることができます。H が 2 回以上出ているケースは 4 通りですね。上のような単純な例では樹形図を書かなくても計算できる方法が知られていますが、状況が複雑になったときには、公式が適用できずに、この樹形図に立ち返って考えなくてはならないことがあります。

積の法則

図のように海辺町から真中町を経由して山奥町へ向かう道順は何通りあるか数えてみましょう。
 

海辺町から真中町までは 3 通りですね。それぞれに対して山奥町に向かう 2 通りの道が選択できるのですから、全ての道順は 3 × 2 = 6 通りとなります。このような状況を一般化した公式が積の法則です。

一般化したので少し難しい言い回しになりましたけど、これをそのまま覚えるのではなく、先ほどの道順のようなイメージを思い浮かべることが大切です。

積の法則の本質を理解するために風変わりな例を１つ載せておきます。
とある日のお昼休みに、サラリーマンの田中さんが「カツ丼、カレーライス、ラーメン」の何を食べようか迷っていました。そしてその日の夕方に、田中さんとは縁もゆかりもない受験生の佐藤君が自宅で「今日は数学と英語、どちらを勉強するべきか」と迷っていました。起こり得る全ての事がらは何通りでしょう？

田中さんと佐藤君には何の接点もなく、互いの決定には何の影響も及ぼしあいません。しかし「カレーライスと英語」、「ラーメンと数学」という現象が必ず生じます。こうした状況で積の法則が適用されるのです。田中さんの「カツ丼、カレーライス、ラーメン」という選択肢１つ１つに対して、佐藤君は「数学、英語」のいずれかを勉強するという選択肢があるので、現実に起こり得る場合の数は 3 × 2 = 6 通りとなります。

和の法則

一方で和の法則は「２つの現象が決して同時に起こり得ない」場合に適用されます。たとえば「赤と青のサイコロを投げて目の和が 3 か 4 になる場合の数」をかぞえてみましょう。「目の和が 3 になる」と「目の和が 4 になる」現象は決して同時に起こりません。ですから、まず「目の和が 3 になる」場合の数をかぞえてみると、
 

 
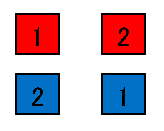
この 2 通りですね。また「目の和が 4 になる」場合の数は
 

 
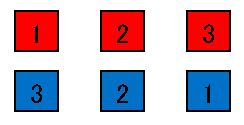
この 3 通りとなります。ですから合わせて 2 + 3 = 5 通りとなります。また少し難しい言い方になってしまいますが、一般化した定理も載せておきます。

確率の分野では「同時に起こり得る」のか「同時には起こり得ない」のかということに常に意識しておく必要があります。