【CL22】直円錐の体積が最大になるような高さと底面半径の比
表面積が一定の直円錐の体積を最大にするように、高さと底面の半径の比を定めてください。
【ヒント】簡単そうに見えて案外手こずる問題です。「何をするか」で迷うことはあまりないはずです。むしろ「どのように計算するか」という工夫が試されます。微分を使うと楽ですけど、別に使わなくても二次関数の知識だけで解けるので、高1でもチャレンジできます。
【解答】下の図で母線 $x$ と高さ $h$ , 底面の半径 $r$ の関係を再確認しておきましょう。
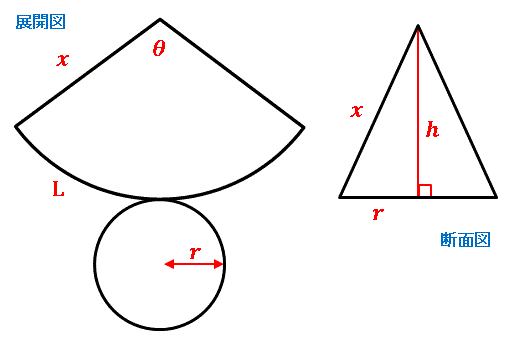
展開図の扇形の弧の長さは底面の円周の長さに等しいので
\[x\theta =2\pi r\]
という関係式を得ることができます。扇形の面積 $T$ と $x$ を半径とする円の面積の比は中心角の比ですから
\[T:\pi x^2=\theta :2\pi\]
すなわち
\[T=\pi x^2 \frac{\theta}{2\pi}=\frac{x\cdot x\theta}{2}\]
$x\theta =2\pi r$ を代入すると
\[T=\pi rx\]
が得られます(これを円錐の側面積の公式としてすでに知っている人はここから解答を始めてください)。直円錐の表面積を $S$ とおくと
\[S=\pi rx+\pi r^2\]
ですから、
\[x=\frac{S-\pi r^2}{\pi r} \tag{A}\]
です。一方で母線と高さ、底円の半径の間には
\[x^2=h^2+r^2\]
という関係があります。ここからが少し計算テクニックを要するところで、
\[h^2=x^2-r^2=(x+r)(x-r)\]
というように因数分解しておきます。$x$ に (A) を入れて計算すると
\[h^2=\frac{S(S-2\pi r^2)}{\pi^2 r^2} \tag{B}\]
が得られます。円錐の体積は
\[V=\frac{1}{3}{\pi r^2h}\]
と表せるので、平方して
\[9V^2=\pi^2 r^4 h^2\]
という形をつくって (B) を代入すると
\[9V^2=r^2 S(S-2\pi r^2)\]
となります。さらに $r^2=t,\:9V^2=f(t)$ とおくと
\[f(t)=tS(S-2\pi t)\tag{C}\]
です。微分すると
\[f'(t)=S(S-4\pi t)\]
となるので最大値をとる $t$ は
\[t=\frac{S}{4\pi}\]
微分を使わない場合は (C) を平方完成して同じように最大値を求められます。この $t=r^2$ を (B) に代入すると
\[h^2=\frac{2S}{\pi}\]
が得られます。$S=4\pi t=4\pi r^2$ なので
\[h^2=8r^2\]
すなわち $h/r=2\sqrt{2}$ であることがわかります。ちなみにおバカな私はスマートな解答を作ることができなかったので、本問の解答作成にあたっては、こちらの記事を参考にさせていただきました。


エクセルや数学に関するコメントをお寄せください
【AI連載小説】数学のリズム、エクセルの旋律(29)
「VBAで直円錐の体積を計算します」
真琴が画面を共有し、「みんな、今日は直円錐の体積を計算するVBA関数を作ってみよう」と言いながら、最初にユーザー定義関数の基本的な形について説明していました。
研伸が質問を投げかけました。
「具体的にどういう風に作るんだ?」
「まず、直円錐の体積計算式を思い出そう。体積(V)は、1/3×底面の面積×高さで計算できるよね」
隆治が手を挙げました。
「それをVBAでどうやって表現するんだい?」
真琴がVBAコードを入力しながら説明します。
「こんな感じですね。」
Function CalcConeVolume(radius As Double, height As Double) As Double CalcConeVolume = (1 / 3) * 3.14159265358979 * radius ^ 2 * height End Function月子が質問しました。
「これで直円錐の体積を計算できるの?」
真琴が頷きました。
「そう。半径と高さを引数に渡すと、それに基づいて直円錐の体積を計算してくれるんだ」