三角級数

三角級数

今回扱うのは次のような三角級数です：
 $$\begin{array}{r}I(\theta )=\sum _{k=0}^n\cos k\theta =\frac{\sin [(n+1)\theta /2]}{\sin (\theta /2)}\cos \frac{n\theta }{2}\\ J(\theta )=\sum _{k=0}^n\sin k\theta =\frac{\sin [(n+1)\theta /2]}{\sin (\theta /2)}\sin \frac{n\theta }{2}\end{array}$$
式だけを眺めていても、$I(\theta )$ や $J(\theta )$ がどんなグラフを描くのかはさっぱり分かりませんから、どうしてもコンピューターの力を借りる必要があります。数値計算においても上の公式のように綺麗にまとまった形は扱いやすくて助かりますね。それではさっそく Excel でグラフを描いてみましょう。

【Excel】coskθの級数

下図は Excel でプロットした三角級数 $I(\theta )$ のグラフです。

 
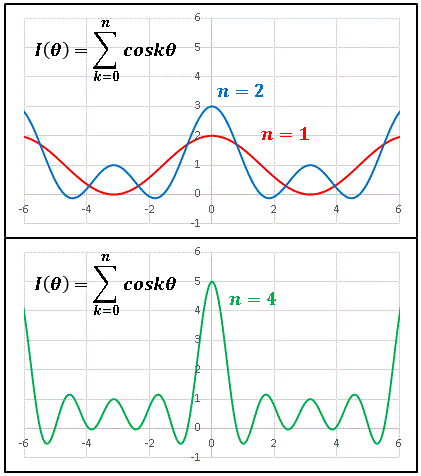
分かりやすいように書き下しておくと、
 $$\begin{array}{rl}& n=1:I=\cos \theta \\ & n=2:I=\cos \theta +\cos 2\theta \\ & n=4:I=\cos \theta +\cos 2\theta +\cos 3\theta +\cos 4\theta \end{array}$$
という関数です。$\cos k\theta$ を次々と足し合わせていくうちに $\theta =2n\pi$ の山の部分が他より突出して高くなっていくことがわかります。$n=8$ で描いてみると…
 

 
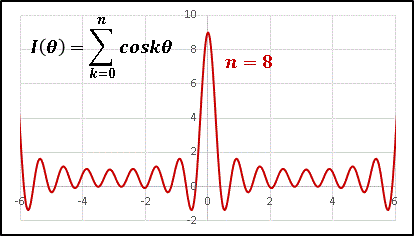
さらにピークの鋭さが増しています。

【Excel】sinkθの級数

下図は Excel でプロットした $J(\theta )$ のグラフです。
 

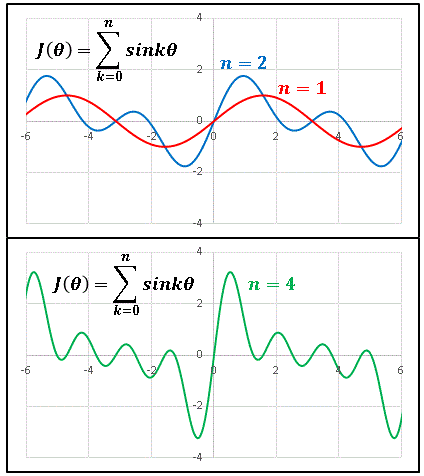
 $$\begin{array}{rl}& n=1:J=\sin \theta \\ & n=2:J=\sin \theta +\sin 2\theta \\ & n=4:J=\sin \theta +\sin 2\theta +\sin 3\theta +\sin 4\theta \end{array}$$
奇関数なので、正負にピークが伸びていきます。
$n=24$ のグラフを確認してみましょう。
 

 
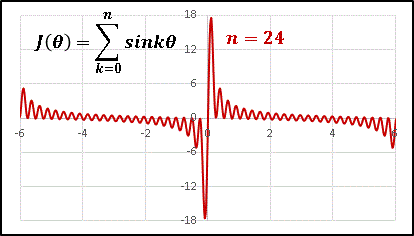
他の振動部分が無視できるほどピークが大きな値をとっています。
$n$ → ∞ の極限では他の波は完全に消え去って、$\theta =2n\pi$ のところにのみ、線のように細く無限大の高さを持つ奇妙な関数となります。

累積関数

次は $\cos kx$ や $\sin kx$ を掛けていったらどうなるかという実験です。$V_n(x)$ と $W_n(x)$ を次のように定義します。
 $$V_n(x)=\prod _{k=1}^n\cos kx,W_n(x)=\prod _{k=1}^n\sin kx$$
ここで Π は「$k$ について全て掛けますよ」という記号です。
高校数学では扱いませんが、要するに Σ の掛け算バージョンです。書き下すと
 $$\begin{array}{r}{V}_n(x)=\cos x\cos 2x\cos 3x\cdots \cos nx\\ W_n(x)=\sin x\sin 2x\sin 3x\cdots \sin nx\end{array}$$
ということです。

まず $V_n(x)$ について $n=3$ から $n=5$ まで動かしてグラフを描いてみます。
 

 
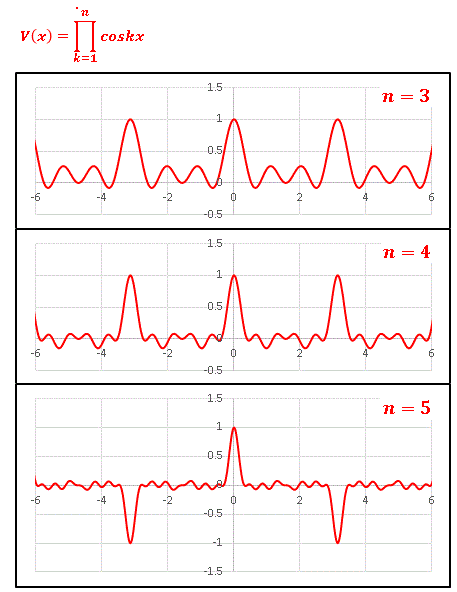
$x=n\pi$ のところに大きな波がありますね。 $n$ が増えるほどそのピークは鋭くなり、他の波は小さくなっていきます。$n=15$ をとると …
 

 
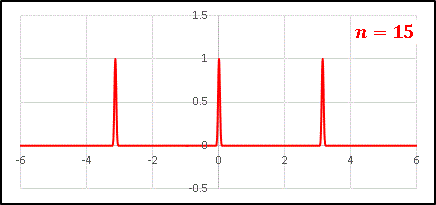
このように他の波は消えてピークだけが残ります。

$\sin kx$ の積 $W_n(x)$ はどのようなグラフを描くでしょうか。
 

 
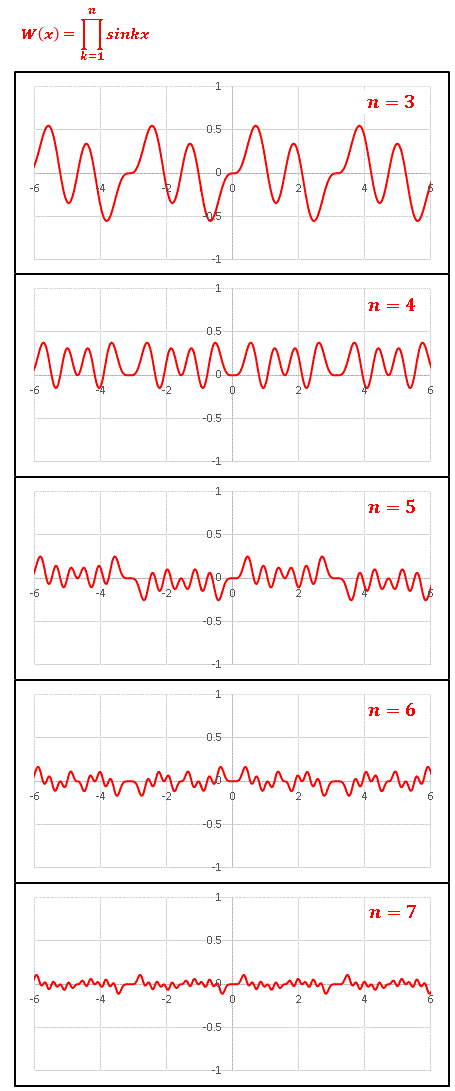
$n$ の増加にともなって全体的な振幅がどんどん減少してますね。
$n=10$ で描いてみると …
 

 
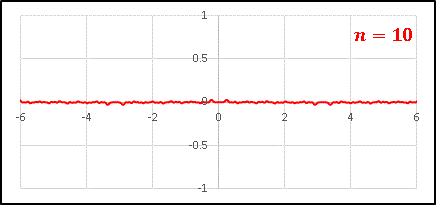
ただのノイズのようになってしまいます。
$n=15$ ぐらいをとると、ほとんど直線と見分けがつかなくなります。

【VBA】累積関数のファンクションマクロ

累積関数を Excel で入力しようとすると

=cos(a1)*cos(2*a1)*cos(3*a1)*cos(4*a1)*cos(5*a1)

のようにたいへん長くて面倒な作業となります。こうした手間を省くために VBA でファンクションマクロ（ユーザー定義関数）を作っておくと便利です。下に $V_n(x)$ と $W_n(x)$ のファンクションマクロを載せておくので、関数を登録しておきたい人は標準モジュールに貼りつけてください。ワークシート関数（エクセル関数）と同じように使えるようになります。それぞれ

=PCOS(xの値, nの値）
=PSIN(xの値, nの値）

という形で入力すると値を返してくれます（x と n の順番に注意！）。

'[VBA] coskxの累積関数
Function PCOS(x As Double, k As Integer) As Double
    PCOS = 1
    For i = 1 To k
        PCOS = PCOS * Cos(i * x)
    Next
End Function
　
'[VBA] sinkx 累積関数
Function PSIN(x As Double, k As Integer) As Double
    PSIN = 1
    For i = 1 To k
        PSIN = PSIN * Sin(i * x)
    Next
End Function