サイクロイド曲線(擺線)
半径 $a$ の円が定直線上を滑らないで転がるとき、この回転円の定点 $P$ が描く曲線の軌跡を サイクロイド曲線(cycloid) あるいは擺線(はいせん) とよびます。サイクロイド曲線はトロコイド(余擺線)とよばれる曲線の一種です。
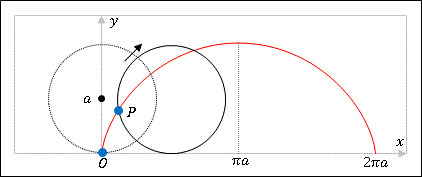
サイクロイド曲線は $t$ を媒介変数として
\[x=a\,(t-\sin t),\:\:y=a\,(1-\cos t)\quad (a\gt 0)\]
という方程式で表すことができます。媒介変数 $t$ に応じて $x,\:\:y$ は
\[\begin{align*}t\::\:0\quad&\Longrightarrow\quad\pi\quad\Longrightarrow\quad 2\pi\\[6pt]x\::\:0\quad&\Longrightarrow\quad\pi a\quad\Longrightarrow\quad 2\pi a\\[6pt]y\::\:0\quad&\Longrightarrow\quad 2a\quad\Longrightarrow\quad 0\\[6pt]\end{align*}\]
のように動いてちょうど1周します。
サイクロイドの面積
サイクロイド曲線の媒介変数表示
\[x=a\,(t-\sin t),\:\:y=a\,(1-\cos t)\quad (a\gt 0)\]
を用いてサイクロイド曲線と $x$ 軸に囲まれた部分の面積を計算できます。$x=\pi a$ で曲線は対称形をしているので、$y$ を $x=\pi a$ まで積分した値を 2 倍します。
\[\begin{align*}S=&\,2\int_{0}^{\pi a}ydx=2\int_{0}^{\pi}y\frac{dx}{dt}\,dt\\[6pt]=&\,2\int_{0}^{\pi}a\,(1-\cos t)\,a\,(1-\cos t)\,dt\\[6pt]=&\,2a^2\int_{0}^{\pi}(1-2\cos t+\cos^2t)\,dt\end{align*}\]
第1項と第2項はそれぞれ
\[\int_{0}^{\pi}dt=\pi,\quad\int_{0}^{\pi}\cos t\,dt=0\]
となります。第3項は $\displaystyle a_n=\int_{0}^{\frac{\pi}{2}}\cos^nt\,dt$ の漸化式
\[a_0=\frac{\pi}{2},\:\:a_1=1,\:\:a_n=\frac{n-1}{n}a_{n-2}\]
によって計算することができます。
\[\int_{0}^{\pi}\cos^2\,dt=2\int_{0}^{\frac{\pi}{2}}\cos^2\,dt=2\cdot\frac{\pi}{4}=\frac{\pi}{2}\]
したがって、求める面積は
\[S=2a^2\,\left(\pi+\frac{\pi}{2}\right)=3\pi a^2\]
となります。
サイクロイド曲線の長さ
$x,\;y$ が媒介変数 $t$ で表されたときの曲線の長さを求める公式は
\[L=\int_{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt\]
です。この公式を使ってサイクロイド曲線
\[x=a\,(t-\sin t),\:\:y=a\,(1-\cos t)\quad (a\gt 0)\]
の長さを計算します。
\[\frac{dx}{dt}dt=a,(1-\cos t)\quad\frac{dy}{dt}=a\,\sin t\]
となるので、求める長さは
\[\begin{align*}L=&\,\int_{0}^{2\pi}\sqrt{2(1-\cos t)}\,dt=\int_{0}^{2\pi}\sqrt{4\sin^2\frac{t}{2}}\,dt\\[6pt]=&\,\int_{0}^{2\pi}\sin\frac{t}{2}\,dt=8a\end{align*}\]
となります。
Excelでサイクロイド曲線を描く
サイクロイド曲線はトロコイド(trochoid)とよばれる曲線群
\[\begin{align*}x&=r_m\theta-r_d\cos\theta\\[6pt]y&=r_m-r_d\cos\theta\end{align*}\]
に含まれます。この方程式で $r_m=r_d$ とおくと、よく知られたサイクロイドの方程式
\[\begin{align*}x&=r_m(\theta-\cos\theta)\\[6pt]y&=r_m(1-\cos\theta)\end{align*}\]
になります。トロコイドを描画するファイルをダウンロードしてください。
ダウンロードを終えたら、ファイルを開いて [トロコイド] のシートを選択します。デフォルトでサイクロイド曲線が描かれているはずです。
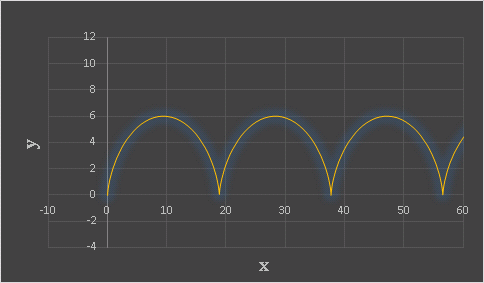
rm = rd に設定したときにサイクロイドになります。rm, rd はスピンボタンを使って自由に変更でるので、色々試してみてください。たとえば rm = 4, rd = 1.5 に設定すると、次のようなトロコイド曲線が描かれます。
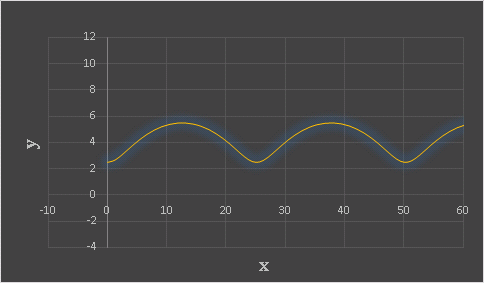

エクセルや数学に関するコメントをお寄せください