ユークリッドの互除法の原理

ユークリッドの互除法

今回は 2000 年も昔から知られるユークリッドの互除法（Euclid’s Algorism）の原理という有名な定理を証明します。

[証明] $a=bq+r\quad (0\leq r\lt b)$ を満たすような $(q,\:r)$ が唯一組だけ存在することは 定理A1 で述べてあります。ここでは
\[(a,\:b)=(b,\:r)\]
が成り立つことを証明します。
\[g_1=(a,\:b),\quad g_2=(b,\:r4)\]
とおきます。$a=bq+r$ なので
\[r=a-bq\]
と書き直すと、$a,\:b$ ともに $g_1$ を約数にもつので、$a,\:b$ の 1 次結合 $r$ もまた $g_1$ を約数にもちます。
\[g_1\:|\:r\]
です。$g_1$ は $b$ と $r$ の公約数なので、$b$ と $r$ の最大公約数以下となっているはずです。
\[g_1\leq g_2\]
同様に $a=bq+r$ において、$b,\:r$ ともに $g_2$ を約数にもつので、その 1 次結合である $a$ も $g_2$ を約数にもちます。すなわち $g_2$ は $a$ と $b$ の公約数なので、$a$ と $b$ の最大公約数以下となっているはずです。
\[g_1\geq g_2\]
$g_1\leq g_2$ かつ $g_1\geq g_2$ なので
\[g_1=g_2\]
が成り立ちます。すなわち
\[(a,\:b)=(b,\:r)\]
が成り立つことが示されました。（証明終）

$a_1\gt a_2\gt 0$ なる 2 整数について、除算アルゴリズムを次々に適用してみます。
\[\begin{align*}&a_1=a_2\,q_1+a_3\quad (0\leq a_3\lt a_2)\\[6pt]&a_2=a_3\,q_2+a_4\quad (0\leq a_4\lt a_3)\\[6pt]&a_3=a_4\,q_3+a_5\quad (0\leq a_5\lt a_4)\\[6pt]&\vdots \end{align*}\]
$a_1\gt a_2\gt a_3\gt\cdots$ なので、いつかは余りが 0 となって割り切れます。それが $n$ 回目であったとすると
\[\begin{align*}&a_3=a_4\,q_3+a_5\quad (0\leq a_5\lt a_4)\\[6pt]&\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\\[6pt]&a_{n-1}=a_n\,q_{n-1}+a_{n+1}\quad (0\leq a_{n+1}\lt a_n)\\[6pt]&a_n=a_{n+1}q_n\end{align*}\]
となります。そこで定理 A12（ユークリッドの互除法の原理）を適用すると
\[(a_1,\:a_2)=(a_2,\:a_3)=(a_3,\:a_4)=\:\cdots\:=(a_n,\:a_{n+1})=a_{n+1}\]
となります。すなわち最後に $a_n$ を割り切った $a_{n+1}$ が最大公約数であるということです。具体的な数でユークリッドの互除法を試してみましょう。556 と 208 の最大公約数を求めてみます。
\[\begin{align*}556&=208\times 2+140\\[6pt]208&=140\times 1+68\\[6pt]140&=68\times 2+4\\[6pt]68&=4\times 17\end{align*}\]
最後に 68 を割り切った 4 が 556 と 208 の最大公約数です。

ユークリッドの互除法を視覚化してみましょう。
例として、72 と 56 の最大公約数を求めます。



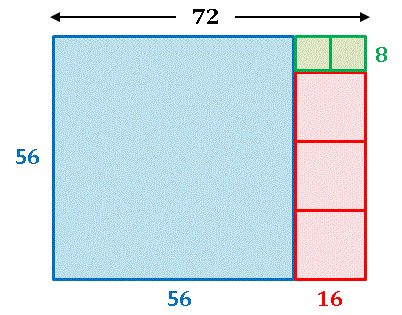
横が 72, 縦が 56 の長方形です。作業は簡単です。まず、この長方形からなるべく大きな正方形ができるように切込みを入れます。１辺の長さ 56 の青い正方形が１つとれましたね。もとの長方形の辺の長さを、この青い正方形の１辺を使って表すと、

72 = 56 × 1 + 16

となります。今度は青い正方形を切り離してしまって、右側の細長い長方形からなるべく大きな正方形がとれるように切込みを入れます。１辺の長さ 16 赤い正方形が 3 つとれます。式で表すと、

56 = 16 × 3 + 8

です。残ったのは１辺の長さ 16 の緑色の長方形で、これは

16 = 8 × 2

と 2 つに分けることができます。もとの長方形は１辺が 8 の正方形タイルできれいに敷き詰めることができます。つまり 72 と 56 の最大公約数は 8 だということです。これが最大公約数の図形的な意味です。上の計算式をまとめて書いてみます。

　　72 = 56 × 1 + 16
　　56 = 16 × 3 + 8
　　16 = 8 × 2

従って、8 が最大公約数であることがわかります。もう少し簡略化して書くと、

　　72 ÷ 56 = 1　[余り 16]
　　56 ÷ 16 = 3　[余り 8]
　　16 ÷ 8 = 2 　[余り 0]

のように計算します。手順は除数（割る数）を余りで割ることの繰返しです。