【Excel】線型合同法による疑似乱数の生成

Excel の RAND 関数や VBA の Rnd 関数も含めて、ほとんどのプログラミング言語には疑似乱数を発生させる関数やライブラリが用意されています。読んで字の如く本物の乱数ではなく「あたかも無作為に並んでいるように見える（実際には周期をもつ）数列」なのですが、そもそもソフトウェアだけでは「本物の乱数」は作れないとされています。とりあえずはこれで代用するしかないのです。

疑似乱数を最も簡単に作れる方法として線型合同法という手法があります。計算手順が簡単でメモリを消費しないというメリットはある一方で、乱数としての質があまり良くないので、高品質の乱数が要求されるシミュレーションや暗号などには使えません。とはいえ、くじ引きやサイコロ、ゲームにおける成否判定ぐらいなら、この方法で十分です。線型合同法による乱数発生数式はとても簡単で、$n$ 番目の乱数は
$$x_{n+1}=(a{x}_n+b)\mathrm{mod}m(m>a,m>b,a>0,b\ge 0)$$
によって与えられます。$X\mathrm{mod}M$ は $X$ を $M$ で割ったときの余りという意味です。初期値 $x_0$ は乱数の種 (Seed) とよばれます。上の数式で発生する乱数は次の条件を満たす場合に最大周期 $m$ を持つことが知られています（もちろん乱数ですから１周期の間の数字しか使えません）。

[1] $b$ と $m$ が互いに素である
[2] $a-1$ が $m$ の全ての素因数で割り切れる
[3] $m$ が 4 の倍数のときは $a-1$ も 4 の倍数である。

最大周期が $m$ なので、実用を考えると $m$ には非常に大きな数を採用する必要があります。たとえば Borland C++ では
$$a=22695477,b=1,m=2^{32}$$
という値を用いています。Excel では、こんな大きな値で計算させるとオーバーフローしてしまうので、ここでは
$$a=13,b=7,m=24$$
という小さな値で線型合同法を試してみることにしましょう。

【Excel】線型合同法で周期24の疑似乱数を生成します

　以下のようなシートを作ってみます。



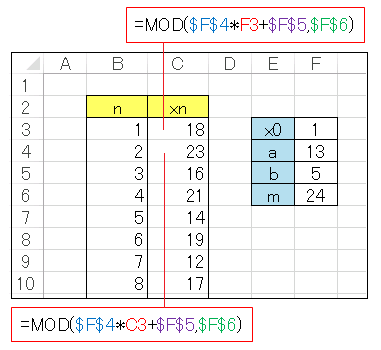
B 列には $n$ の値を 100 個ほど用意してください。
セル F3 ～ F6 に $x_0,a,b,m$ の値を入力します。
セル C3 は初期値 $x_0$ を参照するので

=MOD($F$4*F3+$F$5,$F$6)

と入力しておきます。セル C4 には

=MOD($F$4*C3+$F$5,$F$6)

と入力して末端まで数式をコピーしておきます。すると

20, 3, 22, 5, 0, 7, 2, 9, 4, 11,6, 13,
8, 15, 10, 17, 12, 19, 14, 21, 16, 23, 18, 1
20, 3, 22, 5, 0, 7, 2, 9, 4, 11,6, 13,
8, 15, 10, 17, 12, 19, 14, 21, 16, 23, 18, 1, ...

というように周期 24 で無作為な数値が並びます。