地球と人間が引き合う力（万有引力の法則）

“Measure & Measure” の５回目です。前回までは色々な物のエネルギーを計算しましたが、今回からしばらくは力についてお話したいと思います。

地球と人間が引き合う力

投げたボールが地面に落ちるのは、地球とボールが互いに引き合っているからです。これを引力といいます。そんなことは今どき小学生でも知っていると思いますが、具体的にどのくらいの力になるのかを計算してみましょう。かの有名な物理学者アイザック・ニュートンは２つの物体の間には
\[F=G\frac{m_1m_2}{r^2}\:[\mathrm{N}]\]
という力がはたらくことを発見しました。



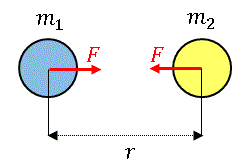
これを万有引力の法則とよびます。単位の N は発見者にちなんでニュートンと読みます。$m_1,\:m_2$ はそれぞれの物体の質量で単位は kg、$r$ は物体の中心間の距離で単位は m です。そして $G$ はとても小さな値の定数で、おおよそ
\[G=6.67\times 10^{-11}\mathrm{m^3kg^{-1}s^{-2}}\]
であることが知られています。万有引力はあまりに弱い力なので普段は感じることはありませんけど、どれほど小さな質量の物体の間にも、この力がはたらいています。たとえば質量 1 kg の英語辞書を 2 冊用意して 1m 離して置くと、
\[F=6.67\times 10^{-11}\:[\mathrm{N}]\]
の力で引き合うわけです。まあ、ほとんど 0 ですけどね。実際、人が感じられるほどの引力をはたらかせるためには、月とか地球のように巨大な質量をもつ必要があります。そこで地球が質量 $m\:\mathrm{kg}$ の物体を引っぱる力を計算してみましょう。

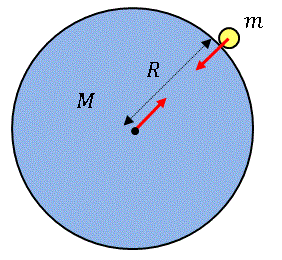
ちなみに地球の質量は
\[M=5.974\times 10^{24}\:[\mathrm{kg}]\]
です。$r$ は物体の中心間の距離なので、たとえ物体が机の上に置かれていようと、富士山のてっぺんにあろうと、地球の赤道半径 6378 km すなわち
\[R=6.387\times 10^6\:[\mathrm{m}]\]
で近似できます。物体と地球の質量、地球の半径を万有引力の公式
\[F=G\frac{m_1m_2}{r^2}\]
に入れて計算すると
\[F=G\frac{Mm}{R^2}=9.8m\:[\mathrm{N}]\]
が得られます。9.8 は重力加速度とよばれる定数で $g$ という記号で表します（単位は $\mathrm{m/s^2}$）。つまり地表近くの物体にはたらく力は
\[F=mg\:[\mathrm{N}]\]
で表すことができます。$g$ をざっくり 10 $\mathrm{m/s^2}$ として、物体の質量に 10 をかければ、地球から引っぱられる（あるいは物体が地球を引っぱる）力を概算できます。

1 kg の英語辞書なら約 10 N の力を受けるし、3 kg の猫ちゃんなら 30 N の力で引っぱられます。体重 50 kg の人間には 約 500 N の力がはたらいていることになります。1 トンの自動車なら 10000 N です。ただし $F=mg$ はあくまで近似式なので、地球と物体の距離があまりに離れすぎると使えません。地球の赤道半径が 6378 km であることを考えると、地表から 100 km とか 200 km ぐらいになってくると、$F=mg$ では無理があります。その場合はもとの万有引力の式で計算します。

万有引力定数の正確な値は？

万有引力定数はあまりに値が小さいので、現代でもなかなか正確に測定できずに、6.67 以下の桁は発表した研究所によってまちまちです。科学の専門書でも、
\[G=6.672\times 10^{-11}\mathrm{m^3kg^{-1}s^{-2}}\]
と記述しているものもあれば、
\[G=6.673\times 10^{-11}\mathrm{m^3kg^{-1}s^{-2}}\]
と書いてあるものもあります。参考までに、2014 年の CODATA (科学技術データ委員会：Committee on Data for Science and Technology) による推奨値を載せておくと、
\[G=6.674\times 10^{-11}\mathrm{m^3kg^{-1}s^{-2}}\]
となっています。どの値を使えばいいのかと迷ってしまいそうですが、別にどれを使っても大差ありませんし、わからないのですから、どの値が正解だと答えようもないのです。