sin^2x の積分, cos^2x の積分, tan^2x の積分
$\sin^2 x,\ \cos^2 x,\ \tan^2 x$ の積分はよく出てきます。
比較的簡単な形をしているので、覚えてしまって損はありません：
\[\begin{align*}\int \mathrm{sin}^{2}xdx&=\frac{x}{2}-\frac{\mathrm{sin}2x}{4}+C\tag{1}\\[6pt]
\int \mathrm{cos}^{2}xdx&=\frac{x}{2}+\frac{\mathrm{sin}2x}{4}+C\tag{2}\\[6pt]
\int \mathrm{tan}^{2}xdx&=\mathrm{tan}x-x+C\tag{3}\end{align*}\]
特に定積分の場合は区間 $[0, \pi/2]$ の積分を１ユニットとして記憶します：
\[\int_{0}^{\pi /2}\mathrm{sin}^{2}xdx=\frac{\pi}{4}\tag{4}\]
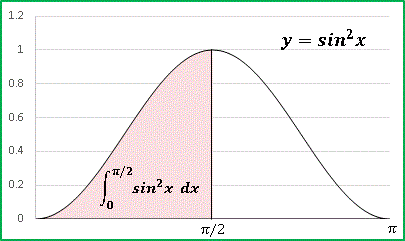
この値を知っていれば、区間 $[0, \pi]$ における積分なら倍の $\pi/2$、区間 $[0, 2\pi]$ における積分であれば 4 倍の $\pi$ を得ることになります（下図参照）。$\cos^2 x$ の積分も区間 $[0, n\pi]$ の積分であれば全く同じ値をとることになります。
余力があれば、(1) ～ (3) をより一般化した次の公式を覚えてください；
\[\begin{align*}\int \mathrm{sin}^{2}mxdx&=\frac{x}{2}-\frac{\mathrm{sin}\, 2mx}{4m}+C\tag{5}\\[6pt]
\int \mathrm{cos}^{2}mxdx&=\frac{x}{2}+\frac{\mathrm{sin}\, 2mx}{4m}+C\tag{6}\\[6pt]
\int \mathrm{tan}^{2}mxdx&=\frac{\mathrm{tan}\, mx}{m}-x+C\tag{7}\end{align*}\]
$\mathrm{cosec}^{2}x,\ \mathrm{sec}^{2}x,\ \mathrm{cot}^{2}x$ の積分はより簡単な形をしています：
\[\begin{align*}&\int \mathrm{cosec}^{2}xdx=-\mathrm{cot}x+C\tag{8}\\[6pt]
&\int \mathrm{sec}^{2}xdx=\mathrm{tan}x+C\tag{9}\\[6pt]
&\int \mathrm{cot}^{2}xdx=-\mathrm{cot}x-x+C\tag{10}\end{align*}\]
$\mathrm{cosec}$ や $\mathrm{sec}$ の記号に慣れない人のために書き直すと次のようになります：
\[\begin{align*}&\int \frac{dx}{\mathrm{sin}^{2}x}=-\frac{1}{\mathrm{tan}x}+C\tag{11}\\[6pt]
&\int \frac{dx}{\mathrm{cos}^{2}x}=\mathrm{tan}x+C\tag{12}\\[6pt]
&\int cot^{2}xdx=-\frac{1}{\mathrm{tan}x}-x+C\tag{13}\end{align*}\]
簡単な計算例を載せておきます：
\[\int \frac{dx}{\mathrm{cos}^{2}\ x\mathrm{sin}^{2}x}=\int \left (\frac{1}{\mathrm{cos}^{2}x}+\frac{1}{\mathrm{sin}^2{x}} \right )dx=\mathrm{tan}x-\mathrm{cot}x+C\]
sin^3x, cos^3x の積分
$\sin^3 x$ と $\cos^3 x$ の積分は意外と覚えやすい形をしています：
\[\begin{align*}\int \mathrm{sin}^{3}xdx=\frac{1}{3}\mathrm{cos}^{3}x-\mathrm{cos}x+C\tag{14}\\[6pt]
\int \mathrm{cos}^{3}xdx=\mathrm{sin}x-\frac{1}{3}\mathrm{sin}^{3}x+C\tag{15}\end{align*}\]
$\sin$ に対しては $\cos$ が、$\cos$ に対しては $\sin$ が式に現れてくるとイメージしておくと覚えやすいです。とくに $0$ から $\pi/2$ までの積分は
\[\int_{0}^{\pi/2} \mathrm{sin}^{3}xdx=\int_{0}^{\pi/2} \mathrm{cos}^{3}xdx=\frac{2}{3}\tag{16}\]
となります。$\sin^2 x$ の積分のときと同様に、上式を 1 ユニットとして区間 $[0,\pi]$, $[0,3\pi/2]$ について計算することも可能ですが、三角関数の指数部分が奇数の場合は負の面積が生じるので単純に定数倍することはできません。
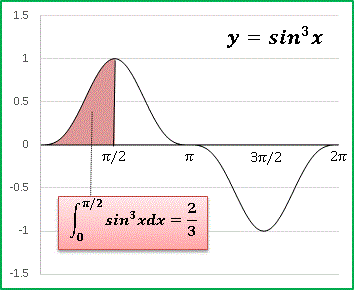
この図から $\sin^3 x$ の定積分に関しては、
\[\begin{align*}&\int_{0}^{\pi} \sin^{3}xdx=\frac{4}{6}\tag{17}\\
&\int_{0}^{3\pi/2} \sin^{3}xdx=\frac{2}{3}\tag{18}\\
&\int_{0}^{2\pi} \sin^{3}xdx=0\tag{19}\end{align*}\]
のような計算が成立します。
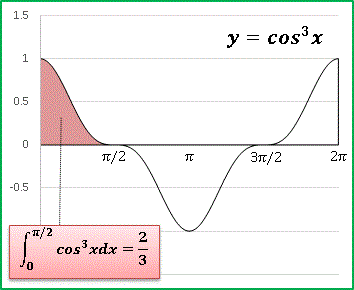
同様に上図から $\cos^3 x$ の定積分は、
\[\begin{align*}&\int_{0}^{\pi} \mathrm{cos}^{3}xdx=0\tag{20}\\
&\int_{0}^{3\pi/2} \mathrm{cos}^{3}xdx=-\frac{2}{3}\tag{21}\\
&\int_{0}^{2\pi} \mathrm{cos}^{3}xdx=0\tag{22}\end{align*}\]
が成り立ちます。図を明確にイメージすれば（というより紙に簡単な図を描いてください）、区間 $[\pi,3\pi/2]$ についても同様の計算が可能です。
エクセルや数学に関するコメントをお寄せください
AIにsin^2xを積分してもらいました
[ChatGPT] sin^2(x)を積分するためには、積分の公式や代替的な方法を使用することができます。sin^2(x)の積分は以下のように計算できます。
∫sin^2(x) dx
sin^2(x)は三角関数の2乗なので、三角恒等式を利用して書き換えることができます。
sin^2(x) = (1 – cos(2x)) / 2
したがって、元の積分は以下のように変形できます。
∫sin^2(x) dx = ∫(1 – cos(2x))/2 dx
この積分は個別の項に分割することができます。
∫(1 – cos(2x))/2 dx = (1/2)∫dx – (1/2)∫cos(2x) dx
第1項はxの積分であり、第2項はcos(2x)の積分です。それぞれ積分すると次のようになります。
(1/2)∫dx = x/2 + C1 （C1は積分定数）
(1/2)∫cos(2x) dx = (1/2)(1/2)sin(2x) + C2 = (1/4)sin(2x) + C2 （C2は積分定数）
したがって、元の積分の答えは次のようになります。
∫sin^2(x) dx = (1/2)x – (1/4)sin(2x) + C （Cは積分定数）
以上がsin^2(x)の積分の手順と答えです。
AIがcos^2xを積分します
[ChatGPT] cos^2xを積分すると、以下のようになります。
∫cos^2x dx
積分の公式に基づいて解いていきます。cos^2xは、三角関数の二乗なので、以下の三角恒等式を使います。
cos^2x = (1 + cos2x) / 2
これを積分に適用すると、
∫cos^2x dx = ∫(1 + cos2x) / 2 dx
分配法則を使って展開すると、
= (1/2) ∫(1 + cos2x) dx
各項ごとに積分すると、
= (1/2) ∫dx + (1/2) ∫cos2x dx
第1項は、∫dx = x + C（積分定数Cを含む一般的な解）です。第2項については、三角関数の積分公式を使います。
∫cos2x dx = (1/2) ∫(1 + cos4x) dx = (1/2) (x/2 + (1/4)sin4x) + C
以上より、cos^2xの積分は次のようになります。
∫cos^2x dx = (1/2) x + (1/4) sin2x + C
ここで、Cは積分定数です。