ガンマ関数の定義と解析接続

ガンマ関数

階乗 $n!$ を複素数にまで拡大定義した関数がガンマ関数です。数学者オイラーによって発見されたので、第２種オイラー積分と呼ばれることもあります。その名のとおり、ガンマ関数は積分によって定義される関数です:
 \[\Gamma(z)=\int_{0}^{\infty}e^{-t}t^{z-1}dt\tag{1}\]
$t$ の指数 $z$ が変数となっていることに注意してください。積分値が下限で収束するためには、$z=x+iy$ の実部が正数である必要があります（$x\gt 0$）。複素数全域で定義する方法は記事の下を参照してください。(1) を部分積分することによってガンマ関数の最も重要な性質を導くことができます。
 \[\begin{align*}\Gamma(z+1)=&\int_{0}^{\infty} e^{-t}t^{z}dt\\[6pt]=&\left[ -e^{-t}t^z\right]_{0}^{\infty}+z\int_{0}^{\infty} e^{-t}t^{z-1}dt=z\Gamma(z)\end{align*}\]
整数や半整数のガンマ関数を計算するためには $\Gamma(1)$ と $\Gamma(1/2)$ の値を知って置く必要があります。(1) は定義にしたがって簡単に計算できます。
 \[\Gamma(1)=\int_{0}^{\infty}e^{-t}dt=1\]
また、$e^{-x^2}$ の積分公式（ガウス積分）
 \[\int_{0}^{\infty }e^{-x^{2}}dx=\frac{\sqrt{\pi}}{2}\]
を用いると $\Gamma(1/2)$ の値を求めることができます。
\[\Gamma\left( \frac{1}{2}\right)=\int_{0}^{\infty} e^{-t}t^{-1/2}dt=\int_{0}^{\infty} \frac{e^{-t}}{\sqrt{t}}dt\]
ここで $t=u^2$ という変数変換をすれば
 \[\Gamma \left(\frac{1}{2}\right)=\int_{0}^{\infty}e^{-u^2}du=\sqrt{\pi}\]
(1) をもとに $\Gamma(n+1)$ を計算できます。
 \[\begin{align*}\Gamma(1)=&\,1\\[6pt]\Gamma(2)=&\,1\cdot\Gamma(1)=1\\[6pt]\Gamma(3)=&\,2\cdot \Gamma(2)=2 \cdot 1\\[6pt]\Gamma(4)=&\,3\cdot\Gamma(3)=3 \cdot 2\cdot 1\\[6pt]&\vdots\\[6pt]\Gamma(n+1)=&\,n\,(n-1)\,(n-2) \cdots 2 \cdot 1 \cdot 1=n!\\[6pt]\end{align*}\]
同様に Γ(1/2) をもとに Γ(n + 1/2) を計算することができます。
 \[\begin{align*}\Gamma\left( n+\frac{1}{2}\right)=&\left(n-\frac{1}{2}\right)\Gamma\left(n-\frac{1}{2}\right)\\[6pt]=&\left(n-\frac{1}{2}\right)\left(n-\frac{3}{2}\right)\cdots\frac{3}{2}\,\frac{1}{2}\,\Gamma\left(\frac{1}{2}\right)\\[6pt]=&\frac{(2n-1)(2n-3)\cdots 3\cdot 1}{2^n} \sqrt{\pi}\\[6pt]=&\frac{(2n-1)!!}{2^n}\sqrt{\pi}\end{align*}\]
最後に現れた「!!」 は「２重階乗」の記号です。
ガンマ関数の公式を下にまとめておきます。
 \[\begin{align*}&\Gamma(z)=\int_{0}^{\infty}e^{-t}t^{z-1}dt\tag{1}\\[6pt]&\Gamma(z+1)=z\Gamma(z)\tag{2}\\[6pt]&\Gamma(1)=1\tag{3}\\[6pt]&\Gamma \left(\frac{1}{2}\right)=\sqrt{\pi}\tag{4}\\[6pt]&\Gamma(n+1)=n! \tag{5}\\[6pt]&\Gamma \left(n+\frac{1}{2}\right)=\frac{(2n-1)!!}{2^n}\sqrt{\pi} \tag{6}\end{align*}\]

解析接続

(1) の積分による定義では $x\gt 0$ に制限されていますが、公式 (2) を使って
 \[\Gamma(z)=\frac{\Gamma(z+1)}{z}\]
と定義しなおすことによって制限を解除することができます。このような定義域の拡大方法を解析接続とよびます。たとえば $z=-1/2$ とおくと
 \[\Gamma(-1/2)=\frac{\Gamma(1/2)}{-1/2}=-\frac{\sqrt{\pi}}{2}\]
というように値を求めることができます。ただし、$z=0$ ではやはり定義できず、そのことによって $z$ が正負の整数の点で定義されません。たとえば $z=-2$ に対しては
 \[\Gamma(-2)=\frac{\Gamma(-1)}{-2}=\frac{1}{-2}\frac{\Gamma(0)}{-1}\]
となるので特異点であることがわかります。実数変数 $x$ のガンマ関数および、複素数平面上の Γ$x+iy$ の絶対値のグラフを下に載せておきます。
 

 
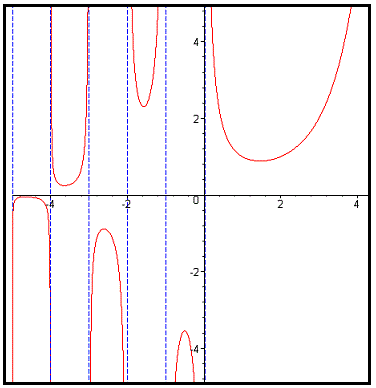
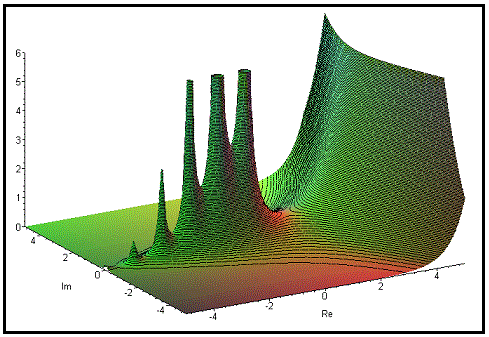
画像は Wikipedia のパブリックドメインのものを使用しています。　

ガンマ関数の被積分関数

変数 $x$ を実数に限定してガンマ関数の被積分関数である
 \[f(t)=e^{-t}t^{x-1}\]
について調べてみます。つまりこの曲線と $t$ 軸によって囲まれる面積がガンマ関数の値となるわけです。ガンマ関数 $\Gamma(x)$ の値の変化はこの面積値の変化ということもできます。エクセルで $f(t)$ のグラフを描いてみます。まず $x\geq 1$ の場合を見てみましょう。
 

 
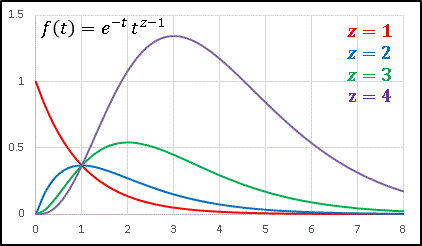
曲線と $t$ 軸によって囲まれる面積は、$x=1$（赤いライン）から、$x=2$（青）、$x=3$（緑）と順次大きくなっています。とくに $x=4$ においては面積は急激に大きくなり、これは先程の $\Gamma(x)$ のグラフにおける値の急増に対応しています。

$e^{-t}$ の部分は $t\rightarrow 1$ で必ず関数を $0$ に収束させますが、$x$ の増加は $t^{x-1}$ の寄与を次第に大きくして、$e^{-t}$ に対抗して極値を $x$ の正方向へ押しやりながら、ピークの値も大きくしているのです。次は $x\leq 1$ の場合のグラフを描いてみます。
 

 
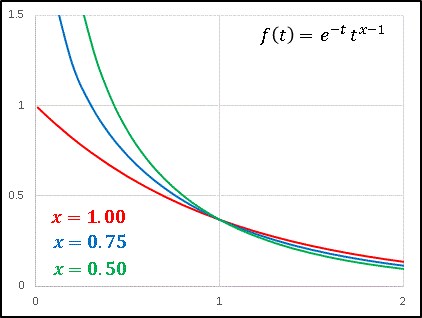
この場合も $x=1.00,\ 0.75,\ 0.50$ となるにつれて面積は増大しますが、$x\geq 1$ のときに比べてさらに変化率が大きくなっています。これは $t$ の指数が負になることによって、$f(t)$ が原点付近でとる値が非常に大きくなるからです。