オイラーの公式
オイラーの公式(Euler’s formula)は指数関数と三角関数、虚数単位を一つに結びつける式です。
\[e^{i\theta}=\cos\theta+i\:\sin\theta\tag{1}\]
(1) で $\theta=\pi$ とすると、有名なオイラーの等式
\[e^{i\pi}=-1\tag{2}\]
を得ます。
【オイラーの公式の証明Ⅰ】正弦関数と余弦関数の級数展開
\[\begin{align*}\cos\theta=1-\frac{1}{2!}\theta^2+\frac{1}{4!}\theta^4-\frac{1}{6!}\theta^6+\:\cdots\cdots \tag{3}\\[8pt]\sin\theta=1-\frac{1}{3!}\theta^3+\frac{1}{5!}\theta^5-\frac{1}{7!}\theta^7+\:\cdots\cdots \tag{4}\end{align*}\]
を用いてオイラーの公式 (1) を証明してみます。
\[\cos\theta+i\:\sin\theta=1+i\theta+\frac{1}{2!}(i\theta)^2+\frac{1}{3!}(i\theta)^3+\cdots\cdots=\sum_{n=0}^\infty(i\theta)^n\tag{5}\]
最後の式は指数関数の級数展開
\[e^x=\sum_{n=0}^\infty x^n\tag{6}\]
において $x$ を $iθ$ に置き換えたものですから、
\[e^{i\theta}=\cos\theta+i\:\sin\theta \tag{7}\]
を得ることができます。さらに、$θ$ を $-iθ$ に置き換えると共役な複素数を得ることができます。
\[e^{-i\theta}=\cos\theta-i\:\sin\theta\tag{8}\]
【オイラーの公式の証明Ⅱ】微分方程式を解く方法がよりスマートです。
\[f(x)=\cos{x}+i\:\sin{x}\tag{9}\]
とおくと $f(0)=1$ です(初期条件)。$f(x)$ を微分すると
\[\frac{df(x)}{dx}=-\sin{x}+i\cos{x}=i(\cos{x}+i\:\sin{x})\tag{10}\]
となるので $f(x)$ は
\[\frac{df(x)}{dx}=if(x)\tag{11}\]
という微分方程式を満たしています。その解は
\[f(x)=Ce^{ix}\tag{12}\]
で ($C$ は定数) 、先ほどの初期条件から
\[f(0)=C=1\tag{13}\]
が決まりますから、
\[f(x)=e^{ix}\tag{14}\]
であることがわかります。よって
\[e^{ix}=\cos{x}+i\:\sin{x}\tag{15}\]
が成り立ちます。■
【Excel】オイラーの等式が成り立つことを確かめます
Excel のエンジニアリング関数を使って、オイラーの等式を確認してみましょう。下の図を参照してください。

上の表は complex_2.xslx ファイルの “オイラーの公式” シートにあるので、必要な方はダウンロードしてください。
≫ complex_2.xlsx をダウンロード
≫ 複素数演算を行なうための Excel 関数については、こちらの記事で説明しています。
まず $e$ の肩に乗る $i\pi$ を計算します。
Excel では、複素数の積は IMPRODUCT 関数で計算できます。セル C4 に
=IMPRODUCT("i",PI())
と入力します。指数部分が複素数となる場合の $e$ のべき乗は IMEXP 関数で計算できます。セル C5 に
=IMEXP(C4)
と入力すると、
-1+3.2311393144413E-15i
が表示されます。数値計算なので若干の誤差が生じていますが、虚数部は無視できるほど小さい数です。
ド・モアブルの定理
オイラーの公式 (1) から ド・モアブルの定理(De Moivre’s theorem)
\[(\cos\theta+i\:\sin\theta)^n=\cos{n\theta}+i\:\sin{n\theta}\tag{16}\]
が導かれます(ただし、$n$ は整数)。
【ド・モアブルの定理の証明】オイラーの公式 $e^{i\theta}=\cos\theta+i\sin\theta$ の両辺を $n$ 乗すると、
\[e^{in\theta}=(\cos\theta+i\sin\theta)^n\tag{17}\]
ここで、左辺は
\[e^{in\theta}=\cos n\theta+i\sin n\theta\tag{18}\]
と表せるので、ド・モアブルの定理
\[(\cos\theta+i\sin\theta)^n=\cos n\theta+i\sin n\theta\tag{19}\]
が成り立ちます。■
ド・モアブルの定理を使って、虚数単位 $i$ の $n$ 乗を求めてみましょう。
\[i=\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}\tag{20}\]
なので、
\[i^n=\cos\frac{n\pi}{2}+i\sin\frac{n\pi}{2}\tag{21}\]
したがって、$i^n$ は以下の 4 つの値のみとることがわかります。
\[i^n=\begin{cases}1&\mathrm{if}\:n=4k\pi\\i&\mathrm{if}\:n=(4k+1)\pi\\
-1&\mathrm{if}\:n=(4k+2)\pi\\i&\mathrm{if}\:n=(4k+3)\pi\\\end{cases}\tag{22}\]
Excel でも確認してみましょう。
下図を参照してデータを作成してください。
$i^n$ を $n=12$ まで計算しています。
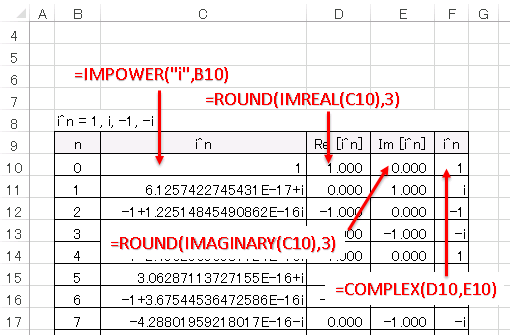
セル C10 には
=IMPOWER("i",B10)
と入力し、オートフィルで C 列に $i^{n}$ のデータを作成していますが、微小な誤差が煩わしくて見づらいので、セル D10 に
=ROUND(IMREAL(C10),3)
と入力し、実部をとってから数値を丸めています。同様にセル E10 には
=ROUND(IMAGINARY(C10),3)
と入力して虚部を丸めます。セル F10 には
=COMPLEX(D10,E10)
と入力して、実部と虚部をあらためて連結しています。Excel の複素数は文字列なので、ROUND など数値を受け取る関数にはそのまま渡せないことに注意してください。上の表は complex.xslx ファイルの “オイラーの公式” シートに載っています。(≫ complex_2.xlsx をダウンロード)
指数関数による三角関数の表現
(7) と (8) を足したり引いたりして、正弦関数や余弦関数を指数関数で表すことができます。
\[\sin\theta=\frac{e^{i\theta}-e^{-i\theta}}{2i},\quad\cos\theta=\frac{e^{i\theta}+e^{-i\theta}}{2}\tag{23}\]
また、上の式を使うと正接関数は次のように表されます。
\[\tan\theta=\frac{e^{i\theta}-e^{-i\theta}}{i(e^{i\theta}+e^{-i\theta})}\tag{24}\]
オイラーの公式の行列表現
オイラーの公式の行列表現を求めてみましょう。虚数に相当する行列は実数成分のみで表されます:
\[I=\begin{pmatrix}0&-1\\1&0\end{pmatrix}\tag{25}\]
実際に行列を計算してみると
\[I^2=-E,\quad I^3=-I,\quad I^4=I\tag{26}\]
となって、確かに虚数としての性質をみたしています。複素数行列は単位行列 E と虚数行列 I を用いて次のように定義します。
\[\begin{align*}Z&=a\:E+b\:I=\begin{pmatrix}a&-b\\b&a\end{pmatrix}\tag{27}\\[8pt]Z^*&=a\:E-b\:I=\begin{pmatrix}a&b\\-b&a\end{pmatrix}\tag{28}\end{align*}\]
$Z^{*}$ は共役複素数行列です。$Z$ と $Z^{*}$ の積を計算すると
\[ZZ^*=Z^*Z=(a^2+b^2)E\tag{29}\]
となっています。
行列型指数関数を級数によって定義します。
\[\begin{align*}e^{\theta I}=&E+(\theta I)+\frac{1}{2!}(\theta I)^2+\frac{1}{3!}(\theta I)^3+\frac{1}{4!}(\theta I)^4+\cdots\cdots\\[8pt]=&E+\theta I-\frac{1}{2!}\theta^2E-\frac{1}{3!}\theta^3I+\frac{1}{4!}\theta^4E\\[8pt]=&E\left(1-\frac{1}{2!}\theta^2+\frac{1}{4!}\theta^4+\cdots\cdots\right)\\[8pt]&+I\left(\theta-\frac{1}{3!}\theta^3+\frac{1}{5!}\theta^5+\cdots\cdots \right)\\[8pt]=&E\:\cos\theta+I\:\sin\theta\end{align*}\tag{30}\]
成分で書くと次のようになります。
\[e^{\theta I}=\begin{pmatrix}\cos\theta&-\sin\theta\\
\sin\theta&\cos\theta\end{pmatrix},\quad e^{-\theta I}=\begin{pmatrix}
\cos\theta&\sin\theta\\-\mathrm{sin}\theta &\cos\theta\end{pmatrix}\tag{31}\]
$e^{\theta I}$ の行列式を計算すると
\[\mathrm{det}\:e^{\theta I}=\cos^2\theta+\sin^2\theta=1\tag{32}\]
となるので、$e^{\theta I}$ の逆行列は共役複素数となります:
\[(e^{\theta I})^{-1}=e^{-\theta I}\tag{33}\]
実際に積を計算してみると
\[e^{\theta I}e^{-\theta I}=e^{-\theta I}e^{\theta I}=E\tag{34}\]
というように単位行列となることが確認できます。
【おすすめ記事】≫ オイラー関数 (オイラーのφ関数)

エクセルや数学に関するコメントをお寄せください