同次式の定義と同次型方程式の解法

同次式

二変数関数 $f(x,y)$ について
 \[f(\lambda x,\lambda y)=\lambda^nf(x,y)\tag{A}\]
が成り立つとき、この関数は 同次式 であるといいます。たとえば $x^2+y^2$ は
 \[(\lambda x)^2+(\lambda y)^2=\lambda ^2(x^2+y^2)\]
となるので同次式です。多項式において全ての項の次数が等しければ (A) が成り立つのは明らかです。

同次型方程式

$n$ 次の同次式
 \[p(x,y)=a_0x^n+a_1x^{n-1}y+a_2x^{n-2}+\cdots+a_ny^n\]
を定義すると
 \[p(\lambda x,\lambda y)=\lambda^np(x,y)\]
が成り立ちます。ここで $\lambda=1/x$ とおくと
 \[p\left(1,\frac{y}{x}\right)=\left(\frac{1}{x}\right)^np(x,y)\]
となるので、
 \[p(x,y)=x^n\left(1,\frac{y}{x}\right)\]
と書き直すことができます。同様に $q(x,y)$ も同次式であるとすれば、$p(x,y)$ と $q(x,y)$ の比は $y/x$ の関数となります。
 \[\frac{p(x,y)}{q(x,y)}=\frac{y}{x}\tag{B}\]
このような理由で、次のような形の微分方程式
 \[\frac{dy}{dx}=\frac{y}{x}\tag{C}\]
を同次型方程式とよびます。同次型方程式を解くときは $y=xu$ とおきます。
\[\frac{dy}{dx}=x\frac{du}{dx}+u\]
となるので、
 \[\frac{du}{dx}=\frac{f(u)-u}{x}\]
変数分離して両辺を積分すると
\[\begin{align*}\int\frac{du}{f(u)-u}&=\int\frac{dx}{x}\\[6pt]\int\frac{du}{f(u)-u}&=\log\,|x|+c\end{align*}\]
$A=\pm e^c$ とおくと
 \[x=A\exp\left[\int\frac{du}{f(u)-u}\right]\]
という解が得られます。$f(u)-u=0$ を満たす $u_0$ が存在すれば $y=u_0x$ も解となります。

p(x,y)とq(x,y)が一次式の場合

$p(x,y),\:q(x,y)$ がともに一次式である場合、つまり
 \[\frac{dy}{dx}=f\left(\frac{ax+by+c}{Ax+By+C}\right)\]
のような形の微分方程式は次のような変数変換によって同次型に帰着することができます。
 \[v=x+m,\quad w=y+n\]
ここで $m,\:n$ はともに定数です。
 \[\frac{dy}{dx}=\frac{dv}{dx}\frac{dy}{dv}=\frac{d}{dv}(w-n)\]
なので、
 \[\begin{align*}ax+by+c&=av+bw-(am+bn-c)\\[6pt]Ax+By+C&=Av+Bw-(Am+Bn-C)\end{align*}\]
ここで定数項が 0 になるように $m,\:n$ を決めます。
 \[\begin{align*}am+bn&=c\\[6pt]Am+Bn&=C\end{align*}\]
行列形式に書き直すと
 \[\begin{pmatrix}a & b\\A & B\end{pmatrix}\begin{pmatrix}m\\ n\end{pmatrix}=\begin{pmatrix}c\\ C\end{pmatrix}\]
$D=aB-bA\neq 0$ のときに逆行列が存在し、
 \[\begin{pmatrix}m\\ n\end{pmatrix}=\frac{1}{aB-bA}\begin{pmatrix}B & -b\\-A & a\end{pmatrix}=\begin{pmatrix}c\\ C\end{pmatrix}\]
すなわち
 \[\begin{pmatrix}m\\ n\end{pmatrix}=\frac{1}{aB-bA}\begin{pmatrix}cB-bC\\aC-cA\end{pmatrix}\]
というように定数を選べば、
 \[\frac{dw}{dv}=f\left(\frac{av+bw}{Av+Bw}\right)=g\left(\frac{w}{v}\right)\]
となって同次型に帰着できます。

同次型方程式の解法例

次のような同次型の微分方程式
 \[\frac{dy}{dx}=\frac{x^2+y^2}{2xy}\tag{D}\]
を解いてみます。$y=ux$ とおくと、
 \[\frac{dy}{dx}=x\frac{du}{dx}+u\]
となるので、(D) に代入すると
 \[x\frac{du}{dx}=\frac{1-u^2}{2u}\tag{D1}\]
となります。変数分離して積分すると
 \[\int\frac{2u}{1-u^2}du=\int\frac{dx}{x}\tag{D2}\]
$u^2-1=z$ とおけば $2udu=dz$ なので左辺は
 \[\int\frac{2u}{1-u^2}du=-\int\frac{dz}{z}=-\log\,|z|\]
となります。右辺は $\log x$ となるので (D – 2) は
 \[-\log\,|z|=\log x+c\]
となります。変数を $z$ から $u$ に戻して整理すると
 \[x(u^2-1)=\pm e^c\]
$A=\pm e^c$ とおくと
 \[u^2=1+\frac{2A}{x}\]
となります。さらに変数を $u$ から $y$ に戻すと
 \[(x+A)^2-y^2=A^2\tag{D3}\]
という解が得られます。
 \[f(u)-u=\frac{1-u^2}{2u}=0\]
に対応する解は $u=\pm 1$ すなわち $y=\pm x$ ですが、これは (D3) で $A=0$ とすれば得られます。よって $A$ を任意定数とすれば (D3) は微分方程式 (D) の一般解となります。解曲線を図示すると次のようになります。
 

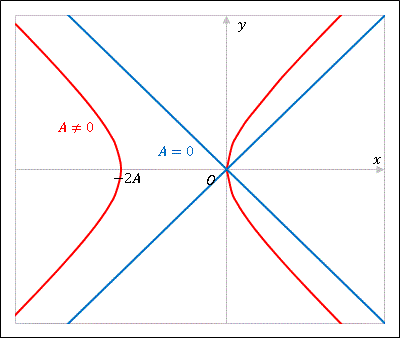
解曲線は $(0,0)$ と $(-2A,0)$ を頂点にもつ直角双曲線群および、直線 $y=\pm x$ です。