既約剰余系

既約剰余系

$m$ を法とする剰余系の１つを
\[\{\;1,\;2,\;\cdots,\;m-1\:\}\]
とします。この集合の要素の中から $m$ と互いに素であるものだけを集めた集合を $m$ を法とする 既約剰余系 といいます。オイラーの関数 $\varphi(m)$ は既約剰余系の要素の個数であるともいえます。

オイラーの定理

$9$ を法とする既約剰余系をつくってみると
\[\{\;1,\;2,\;4,\;5,\;7,\;8\:\}\]
となります。この中の要素を $k$ として
\[a^k\equiv x\quad (\mathrm{mod}\:m)\]
なる $x$ を表に並べてみます。



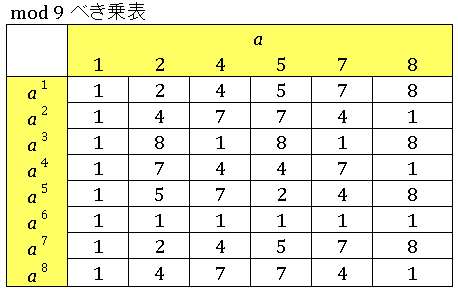
$k$ が $\varphi(9)=6$ のところだけきれいに $1$ が揃っていますね。
すなわち $a^{\varphi(9)}\equiv 1\;(\mathrm{mod}\:9)$ が成り立っています。
これは偶然ではないことが以下の定理でわかります。

[証明] $k=\varphi(m)$ とし、$m$ を法とする既約剰余系を
\[\{\;x_1,\;x_2,\;\cdots\;x_k\:\}\quad (1\leq x_i\leq m,\;i=1,\;2,\;\cdots,\;k)\]
とします。ここで
\[\{\;ax_1,\;ax_2,\;\cdots\;ax_k\:\}\quad (1\leq x_j\leq m,\;j=1,\;2,\;\cdots,\;k)\]
という集合をつくり、

と仮定してみると
\[a(x_j-x_i)\equiv 0\quad (\mathrm{mod}\:m)\]
となります。$(a,\:m)=1$ なので
\[m\,|\,x_j-x_i\]
となるはずですが、これは $1\leq x_j-x_i\leq m-1$ という仮定に反するので不合理です。ゆえに
\[i\neq j\quad\Longrightarrow\quad ax_i\not\equiv ax_j\quad (\mathrm{mod}\:m)\]
となるので、集合
\[\{\;ax_1,\;ax_2,\;\cdots\;ax_k\:\}\quad (1\leq x_j\leq m,\;j=1,\;2,\;\cdots,\;k)\]
は既約剰余系であることになります。したがって
\[(ax_1)\,(ax_2)\,\cdots(ax_k)\,\equiv\, x_1\,x_2\,\cdots x_k\quad (\mathrm{mod}\:m)\]
という合同式が成り立つので
\[(a^k-1)\, x_1\,x_2\,\cdots x_k\,\equiv\,0\quad (\mathrm{mod}\:m)\]
ここで $(x_i,\:m)=1$ より
\[a^k-1\equiv 0\quad (\mathrm{mod}\:m)\]
すなわち
\[a^{\varphi(m)}\equiv 1\quad (\mathrm{mod}\:m)\]
が成り立ちます。（証明終）

法 $9$ であれば $\varphi(9)=6$ なので、計算しなくても表にあるように
\[\begin{align*}1^6\equiv 1\quad (\mathrm{mod}\:9)\\[6pt]2^6\equiv 1\quad (\mathrm{mod}\:9)\\[6pt]4^6\equiv 1\quad (\mathrm{mod}\:9)\\[6pt]5^6\equiv 1\quad (\mathrm{mod}\:9)\\[6pt]7^6\equiv 1\quad (\mathrm{mod}\:9)\\[6pt]8^6\equiv 1\quad (\mathrm{mod}\:9)\\[6pt]\end{align*}\]
が成り立つことがわかるということです。気になる人は関数電卓や Excel で計算してみてください。