硬貨を投げて少なくとも2枚が表となる確率

【PS23】少なくとも２枚が表となる確率

複数の硬貨を投げます。少なくとも2枚が表となる確率を $99$% 以上にするためには何枚以上のコインを投げる必要がありますか？

【ヒント】投げる硬貨の数を $n$ とおいて条件を満たす確率を計算して、その確率が 0.99 を超えるような $n$ を探します。

【考え方】$5$ 枚の硬貨で考えてみます。少なくとも 2 枚が表となる事象の 余事象はすべてが裏または 1 枚だけが表となる事象です。コインの表を H, 裏を T という記号で表して、余事象を列挙すると次のようになります。

T T T T T
H T T T T
T H T T T
T T H T T
T T T H T
T T T T H

すべてが裏となる確率は $\frac{1}{2^5}$ であり、$1$ 枚だけが表となる確率は $\frac{5}{2^5}$ なので、余事象の起こる確率はこれを足し合わせて
$$\frac{1}{2^5}+\frac{5}{2^5}=\frac{6}{2^5}$$
となり、「少なくとも $2$ 枚が表となる」確率は
$$1-\frac{6}{2^5}$$
と表せます。
　
【解答】投げる硬貨の数を $n$ とおきます。「少なくとも $2$ 枚が表となる」事象を $\mathrm{A}$ とすると、その余事象 $\overline{A}$ は「すべてが裏または $1$ 枚だけが表」となります。すべてが裏となる確率は
$$\frac{1}{2^n}$$
であり、$1$ 枚だけが表となる確率は
$$\frac{n}{2^n}$$
なので、余事象 $\overline{A}$ の起こる確率は
$$P(\overline{A})=\frac{1}{2^n}+\frac{n}{2^n}=\frac{n+1}{2^n}$$
となります。したがって、事象 $A$ の起こる確率は
$$P(A)=1-P(\overline{A})=1-\frac{n+1}{2^n}$$
です。この確率が 99% 以上となるのは
$$1-\frac{n+1}{2^n}\ge 0.99$$
という不等式をみたすときです。式を変形すると
$$\frac{2^n}{n+1}\ge 100$$
となります。指数関数は１次関数より速く増加します。$f(x)=2^x$ は $x=1$ のときに $g(x)=x+1$ と交点をもち、$x>1$ では常に $2^x>x+1$ を満たします。すなわち、$2^x/(x+1)$ は $x>1$ で単調増加関数です。参考のために、Excel で描いたグラフを掲載しておきます。

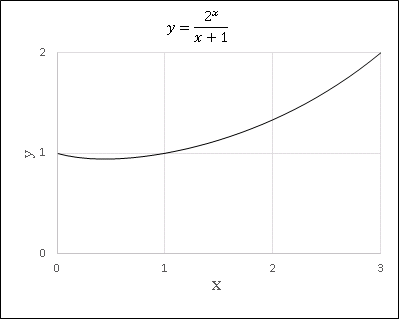
つまり不等式の左辺に適当な $n$ を代入して、左辺が右辺より小さい場合は、それより大きな $n$ を代入する、ということを繰り返せば条件を満たす $n$ を見つけることができます。実際には $n=10$ のときに左辺は $100$ に近い値をとることが予測できるので、とりあえず代入してみると
$$\frac{2^{10}}{10+1}=\frac{1024}{12}=93.1$$
となります。$n=11$ を代入すると
$$\frac{2^{11}}{11+1}=\frac{2048}{12}=170.7$$
となって $100$ を超えます。よって、少なくとも $2$ 枚が表となる確率を $99$ 以上にするには、$11$ 枚以上のコインを投げる必要があることがわかります。

【PS24】進む道をランダムに選びます

東西に延びる道路が南北の道で結ばれている街路があります。


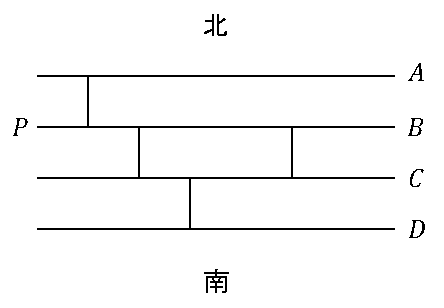
ある人が $P$ 点から東に向かって出発し、以下の規則 [A], [B] にしたがってこの街路を進み、地点 $A,B,C,D$ のいずれかに到達するものとします。

[A] 西から分かれ道に至った場合にはサイコロを振って $1$ か $2$ の目が出たときには東へ進み、それ以外の目が出たときには南北の道へ進みます。
[B] 北または南から分かれ道に至ったときには東へ進みます。

(1) $A$ に到達する確率を求めてください。
(2) $D$ に到達する確率を求めてください。
(3) $B$ または $C$ に到達する確率を求めてください。（センター試験一部改）

【ヒント】まず最初に $A$ や $D$ に到達する経路を調べます。
　
【解答】(1) $D$ に到達するのは下の図の赤い経路です。


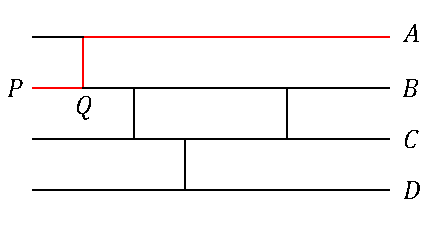
$Q$ で $\frac{2}{3}$ の確率で北の道に向かうので、求める確率は $P(A)=\frac{2}{3}$ となります。
　
(2) $D$ に達するのは下の図の赤い経路です。
　

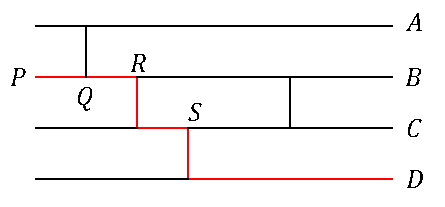
　$Q$ で東へ、$R$ で南へ、$S$ で南へ進むので、求める確率は
　
$$P(D)=\frac{1}{3}\frac{2}{3}\frac{2}{3}=\frac{4}{27}$$
となります。
　
(3)「 $B$ または $C$ に到達する」事象は、「 $A$ または $D$ に到達する」事象の余事象なので、(1) と (2) の結果を用いると、求める確率は
　
$$P(B\cup C)=1-P(A)-P(B)=1-\frac{2}{3}-\frac{4}{27}=\frac{5}{27}$$
となります。

【PS25】1 枚目よりも 2 枚目の数字が大きい確率

　$n$ をある自然数とします。片面に $1$ ～ $n$ の数字が書かれたカードを数字が見えないように伏せて並べます。その中から $1$ 枚を選んで数字を表にして、そのカードをそのままの状態にして、残り $n-1$ 枚のカードから $1$ 枚を選んで数字を表にします。このとき、$2$ 回目に引いたカードに書かれた数字が、最初に引いたカードの数字よりも大きい確率を求めてください。
　
【ヒント】対称性を考えると直感的に $1/2$ になることはわかりますが、それを計算で確かめてみようという問題です。
　
【考え方】最初から $n$ 枚で考えるとイメージしにくいので、$9$ 枚のカードで考えてみます。このとき、たとえば最初に $4$ のカードが選ばれたとします（下図参照）。
　

　
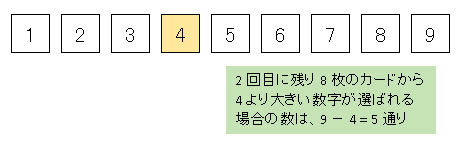
　最初に $4$ のカードを引いて、$2$ 回目に残り $8$ 枚のカードから $4$ より大きな数字 $5,6,7,8,9$ のいずれかを選ぶ確率は
　
$$\frac{1}{9}\frac{9-4}{8}$$
のように計算できます。同様に考えて、最初に $k$ という数字の書かれたカードを選び、$2$ 回目に残り $9-k$ 枚のカードから $k$ より大きな数字のカードを選ぶ確率は
　
$$\frac{1}{9}\frac{9-k}{8}=\frac{9-k}{72}$$
となります。これを $k=1$ から $k=9$ まで足し合わせれば、$2$ 回目に引いたカードに書かれた数字が、最初に引いたカードの数字よりも大きい確率となります：
　
$$\begin{array}{rl}\sum _{k=1}^9\frac{9-k}{72}& =\frac{1}{72}\sum _{k=1}^9(9-k)\\ & =\frac{1}{72}\{9\cdot 9-\frac{9(9+1)}{2}\}=\frac{1}{2}\end{array}$$
　
【解答】最初に $k$ という数字の書かれたカードを選び、$2$ 回目に残り $n-k$ 枚のカードから $k$ より大きな数字のカードを選ぶ確率は
　
$$\frac{1}{n}\frac{n-k}{n-1}=\frac{n-k}{n(n-1)}$$
で計算できます。この式を $k=1$ から $k=n$ まで足し合わせると、求める確率が得られます。
　
$$\begin{array}{rl}\sum _{k=1}^n\frac{9-k}{n(n-1)}& =\frac{1}{n(n-1)}\sum _{k=1}^n(n-k)\\ & =\frac{1}{n(n-1)}\{n^2-\frac{n(n+1)}{2}\}\\ & =\frac{1}{n(n-1)}\frac{n^2-n}{2}=\frac{1}{2}\end{array}$$