必要条件と十分条件、必要十分条件（同値）

必要条件と十分条件

$p⟹q$ が真であるとき、
 
 $p$ は $q$ であるための 十分条件 (sufficient condition)
 $q$ は $p$ であるための 必要条件 (necessary condition)
 
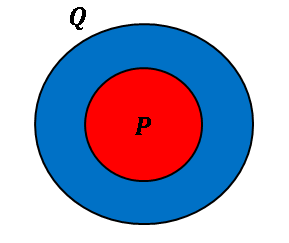
といいます。$p,q$ をみたす要素全体の集合をそれぞれ $P,Q$ とすると、$P\subset Q$ という関係があります。
 

 
たとえば、「$x$ が有理数　$⟹$　$x$ が実数」という命題は真なので、
 
 「$x$ が有理数」は「$x$ が実数」の十分条件
 「$x$ が実数」は「$x$ が有理数」の必要条件
 
となります。
 

 
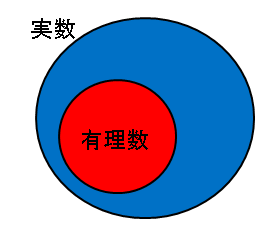
しかし、その逆命題「$x$ が実数　$⟹$　$x$ が有理数」については、$x$ は無理数である場合もあるので偽となります。すなわち
 
 「$x$ が実数」は「$x$ が有理数」の十分条件ではない
 「$x$ が有理数」は「$x$ が実数」の必要条件ではない
 
ということになります。
 
$p,q$ が「$p⟹q$」、およびその逆命題「$q⟹p$」をともに満たすとき、
 
 $p$ は $q$ であるための 必要十分条件
 
とよび、「$p⟺q$」と表します。$p,q$ をみたす要素全体の集合をそれぞれ $P,Q$ について、$P\subset Q,Q\subset P$ という関係にあるので、この２つの集合は完全に一致します。つまり $p$ も $q$ も同じことを述べているに過ぎないので、「$p$ と $q$ は同値である」と表現することもあります。たとえば、実数について次の命題
 $$a^2=b^2⟹|a|=|b|$$
を調べてみましょう。$a^2=b^2$ より $a=\pm b$ です。両辺の絶対値をとると $|a|=|b|$ となるので、この命題は真です。また、逆命題
 $$|a|=|b|⟹a^2=b^2$$
については、$|a|=|b|$ の両辺を 2 乗すると $a^2=b^2$ となるので、これも成立しています。よって
 
 $a^2=b^2$ は $|a|=|b|$ であるための必要十分条件
 
となります。
 
【例題】下の（ア）、（イ）、（ウ）に入る言葉を
 ① 必要十分条件である
 ② 必要条件であるが、十分条件ではない
 ③ 十分条件であるが、必要条件ではない
から選んでください。同じ言葉を選んでも構いません。
 
 自然数 $n$ に対する条件 $p,q,r,s$ を次のように定めます。
 
 $p$：$n$ を $5$ で割ると $1$ 余る
 $q$：$n$ を $10$ で割ると $1$ 余る
 $r$：$n$ は 奇数
 $s$：$n$ は $2$ より大きい素数
 
 このとき、
 「$p\wedge r$」は $q$ であるための（　ア　）。
 $\overline{r}$ は $\overline{s}$ であるための（　イ　）。
 「$p\wedge s$」は「$q\wedge s$」であるための（　ウ　）。（センター試験　１部改）

【解答】条件 $p$ を満たす数は $5s+1$、条件 $q$ を満たす数は $10t+1$（$s,t$ は非負整数）のように表せます。それぞれ並べてみると
 $$\begin{array}{rl}& 1,6,11,16,21,26,31,36,41\cdots \\ & 1,11,21,31,41,51,61,71,81\cdots \end{array}$$
のようになっています。つまり、$5s+1$ から偶数要素を取り除いた集合が $10t+1$ の集合となっています。「$p\wedge r$」を満たす数は「$5$ で割っても $10$ であっても $1$ 余る数なので、$n=10t+1$ となります。つまり
 $$p\wedge r⟹q$$
は真です。またその逆命題である
 $$q⟹p\wedge r$$
も真なので、（ア）は ① の「必要十分条件」です。
 
$\overline{r}$ および $\overline{s}$ はそれぞれ
 $\overline{r}$ ： $n$ は偶数である
 $\overline{s}$ ： $n$ は偶数または素数以外の奇数
となります。したがって $\overline{r}⟹\overline{s}$ は真ですが、その逆は偽となります。よって（イ）は ② の「十分条件であるが必要条件ではない」ということになります。
 
 $p\wedge s$ および $q\wedge s$ はそれぞれ
 $p\wedge s$ ： $5$ で割って $1$ 余る素数
 $q\wedge s$ ： $10$ で割って $1$ 余る素数
 
となります。最初に述べたように、$5s+1$ と $10t+1$ は
 $$\begin{array}{rl}& 1,6,11,16,21,26,31,36,41\cdots \\ & 1,11,21,31,41,51,61,71,81\cdots \end{array}$$
というように、$5s+1$ から偶数を取り除いた集合が $10t+1$ の集合となっているので、それぞれから素数を選び出して集合をつくると同じものになります。したがって
 $$p\wedge s⟺q\wedge s$$
となり、（ウ）は ① の「必要十分条件」です。