周期関数の定義と性質、鋸歯状波

周期関数

関数 $f(x)$ が
 \[f(x+T)=f(x)\quad(T\gt 0)\]
を満たすとき、$f(x)$ は周期 $T$ の 周期関数 (periodic function) であるといいます。また、上式を満たす最小の $T$ を基本周期（fundamental period）といいます。

周期関数の性質

周期関数には次のような性質があります。

ほぼ自明のことですが、いちおう証明しておきます。
 \[\begin{align*}p(x+T)&=af(x+T)+bg(x+T)=af(x)+bg(x)=p(x)\\[6pt]q(x+T)&=f(x+T)g(x+T)=f(x)g(x)=q(x)\end{align*}\]
また、周期関数の積分について次のような性質があります。

これもほとんど自明のことに思えますが、置換積分を使って証明しておきます。積分
 \[\int_{c}^{c+T}f(t)dt\]
において $x=t-c$ とおくと、$t:c\rightarrow c+T$ のとき $x:0\rightarrow T$ となるので、
 \[\int_{c}^{c+T}f(t)dt=\int_{0}^{T}f(x)dx\]
が成り立ちます。

三角関数の周期性

最も有名な周期関数は三角関数で、たとえば $\sin x$ は $2n\pi\quad (n=0,1,2,\cdots)$ の周期をもっています。
 \[\sin(x+2n\pi)=\sin x\quad (n=0,1,2,\cdots)\]
最小周期は $T=2\pi$ です。
もちろん三角関数同士の和や積も周期関数となっています。たとえば
 \[f(x)=\sin\frac{\pi}{2}+\sin\frac{\pi}{3}\]
という関数を考えると、$\sin x/2$ の最小周期は $4\pi$ , $\sin x/3$ の最小周期は $6\pi$ なので、$f(x)$ の最小周期は $4\pi$ と $6\pi$ の最小公倍数である $12\pi$ です。実際に確認してみると
 \[f(x+12\pi)=\sin\frac{x+12\pi}{2}+\sin\frac{x+12\pi}{3}=\sin\frac{\pi}{2}+\sin\frac{\pi}{3}\]
となって、確かに周期が $12\pi$ であることがわかります。

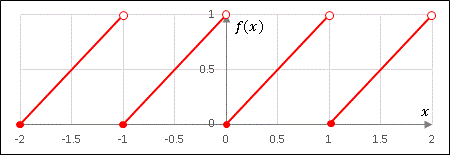
鋸歯状波

他にも単純な周期関数の例として、鋸歯状波
 \[f(x)=x-\lfloor x\rfloor\]
があります。ここに $\lfloor x\rfloor$ はガウス記号で、$x$ を超えない最大の整数を意味しています。この関数は次のように周期 1 で同じ形の線分を連ねた周期関数となります。
 

非周期関数の周期関数への拡張

ある有限区間で定義された適当な関数 $f(x)$ をもってきて、
 \[\tilde{f}(x+nT)=f(x)\quad (0\leq x\lt T,\quad n=\cdots-1,0,1,\cdots)\]
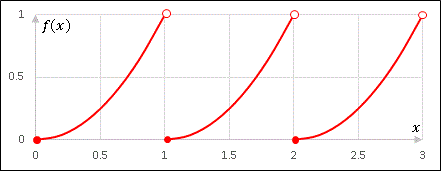
となるようにつなげると、周期関数 $\tilde{f}(x)$ となります。このような拡張の仕方を周期的拡張といいます。たとえば $0\leq x\lt 1$ で定義された二次関数
 \[f(x)=x^2\quad (0\leq x\lt 1)\]
を用意して、
 \[\tilde{f}(x+n)=f(x)\quad (0\leq x\lt 1,\quad n=\cdots-1,0,1,\cdots)\]
のように定義すれば、下の図のような周期関数となります（Excelでプロットしました）。
 

Excelにおける周期関数の取り扱いの注意

Excel には SIN や COS などいくつかの三角関数用意されていますが、これらの関数を用いて数値計算をするときに注意しなくてはならないことがあります。よく知られているように $\sin x$ は
 \[\sin (x+2\pi)=\sin x\]
という周期的性質を満たしているので、$x=0$ とすると
 \[\sin 0=\sin 2\pi=0\]
となるわけですが、これを Excel でそれぞれ

=SIN(0)
=SIN(2*PI())

と入力して計算させて、指数形式で表示すると

0.00E+00
-2.45E-16

という値となります。つまり SIN(2*PI()) は正確に 0 を返しません。その原因は２つあります。１つは引数に用いている PI() が円周率の近似値を返す関数だということです（円周率は無理数なので、コンピュータで正確な値を扱うことはできません）。もう１つの原因は Excel 内部では三角関数をマクローリン級数によって計算しているということです。もちろん有限項で打ち切るので近似計算となります。したがって引数が有理数であっても、その値が大きくなればなるほど、やはり誤差が大きくなるということです。いずれにしても、本来 0 が返るべきところで 0 以外の値が戻ってくるということは、（存在しないはずの SIN(0) の逆数が出力されるなど）場合によっては重大なミスを生じる可能性があるので、Excel では周期関数が正確な値を返さないということを頭の片隅に置いておく必要があります。