三角形の頂点Pの極限の位置を求めます

【CL06】三角形の頂点 P の極限の位置

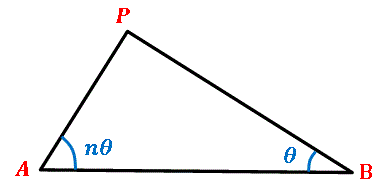　図のような三角形 $ABP$ があり、$\angle A=n\theta,\ \angle B=\theta$ とします。底辺 $AB$ を固定しておいて $\theta\rightarrow 0$ としたとき、頂点 $\boldsymbol{P}$ の極限の位置 を求めてください。
　
　
　
　
【ヒント】図をじっと見つめてみると、$n$ を大きくしたら $P$ は左へ寄るし、$n$ を小さくしたら右へ移動しますね。だから、最終的に $P$ がどこにくるのか、なんとなく予想できます。
　

坂田アキラの ベクトルが面白いほどわかる本 新品価格 ￥1,287から (2022/7/14 21:12時点)

【解答】$AB = a$ とおきます。$\angle P=\pi-n\theta$ なので、正弦定理より
　
\[\frac{AP}{\sin \theta}=\frac{a}{\sin (\pi-n\theta)}=\frac{a}{\sin n\theta}\]
が成り立つので、
　
\[AP=\frac{\sin \theta}{\sin n\theta}\]
と表せます。$\theta\rightarrow 0$ の極限をとると
　
\[\lim_{\theta \rightarrow 0}=\lim_{\theta \rightarrow 0} \frac{n\theta}{\sin n\theta} \frac{\sin \theta}{\theta}\frac{a}{n}=\frac{a}{n}\]
となります。すなわち点 P は AB を 1：n に内分する点です。