確率の基本性質（加法公式・排反事象・余事象）

確率の加法公式

標本空間 $S$ の事象 $E$ に含まれる根源事象の数 $n(E)$ は
 $$0\le n(E)\le n(S)$$
を満たす数です。$n(E)=0$ となるのは $E$ が決して起こらない事象であるときで、このような事象を 空事象 (empty event) とよび、$\varphi$ という記号で表します。また両辺を $n(S)$ で割ると
 $$0\le \frac{n(E)}{n(S)}\le 1$$　すなわち
 $$0\le P(E)\le 1$$
が成り立ちます。$P(E)=0$ となるのは $E=\varphi$、つまり事象 $E$ が決して起こらないときです。たとえばサイコロを振って「 7 の目が出る」というような事象の確率が 0 であることを示しています。また $P(E)=1$ となるのは $E=S$ 、すなわち事象 $E$ が常に起こるときです。サイコロを振って「 1 ～ 6 のいずれかの目が出る」確率が 1 であることを示しています。

$S$ の中に 2 つの事象 $A,B$ があることを考えます。
「$A,B$ がともに起こる事象」を 積事象 (product event) とよび、集合の記号を用いて $A\cap B$ で表されます。これは事象 $A,B$ の共通部分を表しています。また「$A,B$ の少なくとも一方が起こる事象」を 和事象 (sum event) とよび $A\cup B$ で表します。これは事象 $A,B$ の和集合に当たります。
 

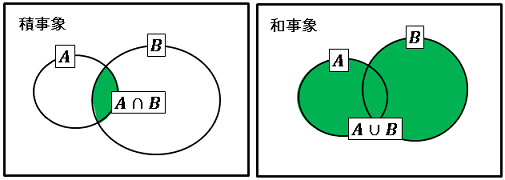
集合の要素の個数について
 $$n(A\cup B)=n(A)+n(B)-n(A\cap B)$$
が成り立つので、両辺を $n(S)$ で割ると
 $$\frac{n(A\cup B)}{n(U)}=\frac{n(A)}{n(U)}+\frac{n(B)}{n(U)}-\frac{n(A\cap B)}{n(U)}$$
となります。すなわち 加法公式
 $$\begin{array}{}\text{(A)}& P(A\cup B)=P(A)+P(B)-P(A\cap B)\end{array}$$
が成り立ちます。ジョーカーを含めた 53 枚のトランプから 1 枚を無作為に取り出して、そのカードが「ハートまたは絵札である」という確率を計算してみましょう。トランプの 52 枚のカードはスペード、ハート、クラブ、ダイヤの 4 種類 13 枚ずつからなり、それぞれに 3 枚ずつ、合計 12 枚の絵札があります。「ハートである」という事象を $A$ , 「絵札である」という事象を $B$ とすると、それぞれの事象の要素数は
 $$n(A)=13,n(B)=12$$
です。またハートの絵札である事象の数は
 $$n(A\cap B)=3$$
です。よって「ハートまたは絵札である」確率は
 $$\begin{array}{rl}P(A\cup B)& =P(A)+P(B)-P(A\cap B)\\ & =\frac{13}{53}+\frac{12}{53}-\frac{3}{53}=\frac{22}{53}\end{array}$$となります。

排反事象

1 つのサイコロを投げるとき、「奇数の目が出る」という事象を $A$ , 「2 の目が出る」という事象を $B$ とすると、$A$ か $B$ のどちらか一方が生じた場合は、他方は決して起こることがありません。
 

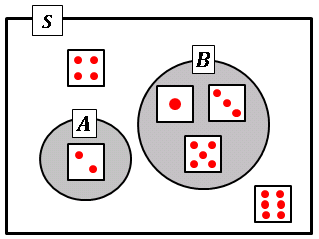
このように複数の事象があって、その中の１つが起これば、他の事象が起こらないとき、これらの事象は 互いに排反する、あるいは 排反事象である といいます。そして $A$ と $B$ が互いに排反であることを
 $$A\cap B=\varphi$$
と表すことができ、$P(A\cap B)=0$ なので、加法公式 (A) より
 $$\begin{array}{}\text{(B)}& P(A\cup B)=P(A)+P(B)\end{array}$$
となります。

余事象

ある事象について「$E$ が起こらない」という事象を $E$ の 余事象 (complementary event) とよび、これは
 $$E\cap \overline{E}=\varphi ,E\cup \overline{E}=U$$
という関係を満たしています（つまり $E$ でなければ $\overline{E}$ , $\overline{E}$ でなければ $E$ です）。
 

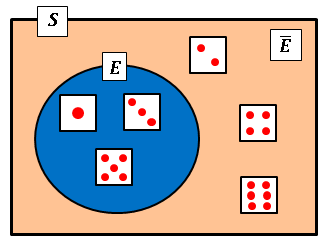
たとえば１つのサイコロを投げるとき、「奇数の目が出る」という事象 $E$ の余事象 $\overline{E}$ は「偶数が出る」です。加法定理より
 $$P(E\cup \overline{E})=P(E)+P(\overline{E})$$
$E\cup \overline{E}=S$ なので、$P(E\cup \overline{E})=P(S)=1$ となり
 $$\begin{array}{}\text{(C)}& P(\overline{E})=1-P(E)\end{array}$$
という公式が得られます。
 

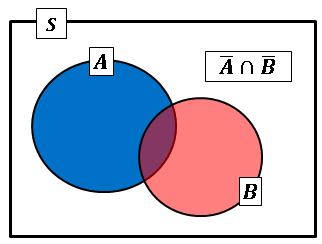
また上のベン図から
 $$\overline{A}\cup \overline{B}=\overline{A}\cap \overline{B}$$
なので、公式 (C) で $E$ の代わりに $\overline{A}\cup \overline{B}$ を代入すると
 $$\begin{array}{}\text{(D)}& P(\overline{A}\cap \overline{B})=1-P(A\cup B)\end{array}$$
が成り立ちます。3 枚の硬貨を投げて「少なくとも 1 枚は表である」事象 $A$ の確率を計算してみましょう。余事象 $\overline{A}$ は「出る目は全て表」ですから、求める確率は
 $$P(A)=1-\frac{1}{2^3}=\frac{7}{8}$$
となります。

確率の単調性

下図のように事象 $B$ が事象 $A$ に含まれているような状況を考えます。
 

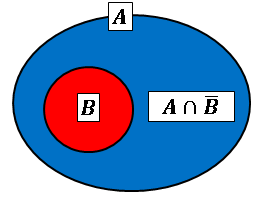
このとき事象 $A$ は
 $$A=B\cup (A\cap \overline{B})$$
と表せるので、
 $$P(A)=P(B)+P(A\cap \overline{B})$$
$P(A\cap \overline{B})\le 0$ なので
 $$P(A)-P(B)\ge 0$$
すなわち確率の単調性

が成り立ちます。これは、ある事象が起こる確率は、その部分事象が起こる確率よりも小さくはないことを示しています。

根源事象の確率の総和

　ある標本空間 $S$ が根源事象 $E_i(i=1,2,\cdots n)$ から成り立っているとします。
 $$S=E_1\cup E_2\cup \cdots \cup E_n$$
よっていずれかの根源事象が起こる確率は
 $$P(S)=P(E_1)+P(E_2)+\cdots +P(E_n)$$
となります。$P(S)=1$ なので
 $$\sum _{i=1}^{n}P(E_i)=P(E_1)+P(E_2)+\cdots +P(E_n)=1$$
が成り立ちます。これを 完全確率の定理 といいます。たとえば、サイコロを投げて、その根源事象（1 の目が出る、2 の目が出る、… 6 の目が出る）の確率の総和を計算すると
 $$\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=1$$
となります。