平方剰余と平方非剰余

平方剰余と平方非剰余

完全平方数
\[1,\;4,\;9,\;16,\;25,\;36,\;49,\;64,\;81,\;\cdots\]
を 3 で割った余りを並べてみると…
\[1,\;1,\;0,\;1,\;1,\;0,\;1,\;1,\;0,\;\cdots\]
というように $1,\;1,\;0$ が周期的に並びます。つまり、どのような平方数も $3$ で割ったときの余りは $0$ か $1$ のどちらかであるということです。上の例については
\[n=3k-2,\quad 3k-1,\quad 3k\quad (k=1,\;2,\;\cdots)\]
をそれぞれ平方してみれば
\[9k^2-12k+4,\quad 9k^2-6k+1,\quad 9k^2\]
となるので、$3$ で割ると余りが
\[1,\;1,\;0,\;1,\;1,\;0,\;1,\;1,\;0,\;\cdots\]
というように交互に並ぶことがわかります。以上の事実は合同方程式
\[x^2\equiv a\quad (\mathrm{mod}\:3)\]
は $a$ が $1$ または $0$ のときに限って解をもつということを示していて、
\[x^2\equiv 2\quad (\mathrm{mod}\:3)\]
には解がない（余りが $2$ となることはない）ということです。平方数を素数で割ったときの余りを表にしてみると次のようになります。

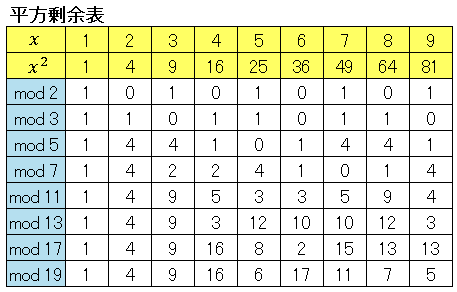
表を眺めてみると、たとえば平方数を $7$ で割ったときの余りは $0$ を除けば $1,\;2,\;4$ に限られていることがわかります。以上の事実を踏まえて、平方剰余と平方非剰余を次のように定義します。

$a$ を正整数と定義しているので、$0$ は平方剰余の定義から外します。たとえば $\mathrm{mod}\:3$ の平方剰余は $a=1$ であり、平方非剰余は $a=2$ ということになります。また、$\mathrm{mod}\:7$ の平方剰余は $a=1,\;2,\;4$ であり、平方非剰余は $a=3,\;5,\;6$ となります。$1^2\equiv 1\quad (\mathrm{mod}\:p)$ なので、$1$ は法の選択に関わらず常に平方剰余です。また、
\[x^2\equiv (p-x)^2\quad (\mathrm{mod}\:p)\]
が成り立つので、平方剰余の個数は $(p-1)/2$ 個であり、たとえば $p=7$ の場合は $(p-1)/2=3$ なので、$1$ から $3$ まで平方して
\[\begin{align*}1^2\equiv 1\quad (\mathrm{mod}\:7)\\[6pt]
2^2\equiv 4\quad (\mathrm{mod}\:7)\\[6pt]
3^2\equiv 2\quad (\mathrm{mod}\:7)\end{align*}\]
これですべての平方剰余が出揃ったことになります。上の表でも各法で $x=(p-1)/2$ のところで平方剰余が揃うことを確認しておいてください。次回以降の記事では様々な定理を使って、この平方剰余／平方非剰余について詳しく調べていきます。

平方剰余であるための必要十分条件

定理 F5 を再掲します。

この定理において $p$ を奇素数、$n=2$ とすると、$p-1$ は偶数なので
\[d=(n,\:p-1)=(2,\:p-1)=2\]
となり、次の定理が得られます。

平方非剰余であるための必要十分条件も調べておきます。
フェルマーの小定理 $a^{p-1}\equiv 1\;(\mathrm{mod}\:p)$ より、
\[\left(a^{\frac{p-1}{2}}-1\right)\,\left(a^{\frac{p-1}{2}}+1\right)\equiv 0\quad (\mathrm{mod}\:p)\]
平方非剰余なので、
\[a^{\frac{p-1}{2}}\not\equiv 1\quad (\mathrm{mod}\:p)\]
したがって次の定理が成り立ちます。

定理 F6 と F7 によると $a^{\frac{p-1}{2}}$ は $1$ か $-1$ のどちらかの値しかとりません。
$1$ であれば平方剰余、$-1$ でれば平方非剰余となります。
法 $11$ で確認してみます。$(p-1)/2=5$ なので
\[\begin{align*}&1^5\equiv 1\quad (\mathrm{mod}\:11)\\[6pt]&2^5=32\equiv -1\quad (\mathrm{mod}\:11)\\[6pt]&3^5=243\equiv 1\quad (\mathrm{mod}\:11)\\[6pt]&4^5=(2^5)^2= (2^5)^2=(-1)^2\equiv 1\quad (\mathrm{mod}\:11)\\[6pt]&5^5=25\times 125=3\times 4=12\equiv 1\quad (\mathrm{mod}\:11)\\[6pt]&6^5=6\times 36\times 36\equiv -5\times 3\times 3=-45\equiv -1\quad (\mathrm{mod}\:11)\\[6pt]&7^5=7\times 49\times 49\equiv -4\times 5\times 5=-100\equiv -1\quad (\mathrm{mod}\:11)\\[6pt]&8^5=8\times 64\times 64\equiv -3\times 9\times 9\equiv -3\times 4\equiv -1\quad (\mathrm{mod}\:11)\\[6pt]&9^5=(3^2)^5=(3^5)^2=1^2\equiv 1\quad (\mathrm{mod}\:11)\\[6pt]&10^5=10\times 10\times 100\equiv -1\times 1\times 1\equiv -1\quad (\mathrm{mod}\:11)\end{align*}\]
したがって、法 $11$ の平方剰余は $1,\;3,\;4,\;5,\;9$ であり、その他は平方非剰余となります。

平方剰余の乗算表

平方剰余同士、平方非剰余同士、あるいは平方剰余と平方非剰余の積がどのようになるのかを乗算表をつくって調べてみます。まず最初に「平方剰余 × 平方剰余」を $11$ で割った余りを表に並べてみます。



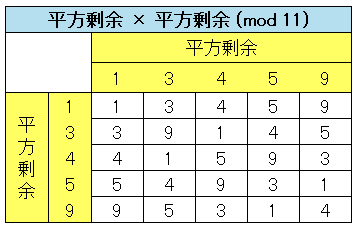
見ての通り、平方剰余同士の積をつくると $1,\;3,\;4,\;5,\;9$ だけが並びます。すなわち

平方剰余 × 平方剰余 = 平方剰余

となっています。次は平方非剰余同士の積です。



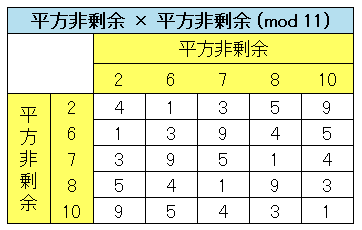
この場合も $1,\;3,\;4,\;5,\;9$ だけが並びます。すなわち

平方非剰余 × 平方非剰余 = 平方剰余

です。最後に平方剰余と平方非剰余の積を調べてみます。



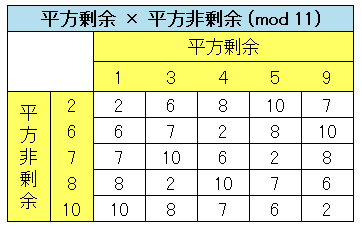
今度は $2,\;6,\;7,\;8,\;10$ だけが並んでいます。すなわち

平方剰余 × 平方非剰余 = 平方非剰余

となっています。

平方剰余同士の積は平方剰余です

一般に以下の定理が成り立ちます。

[証明] 前回記事の定理 F6 と F7 を用います：

(1) $a,\;b$ がともに平方剰余なので
\[(ab)^{\frac{p-1}{2}}=a^{\frac{p-1}{2}}\,b^{\frac{p-1}{2}}\equiv 1\cdot 1=1\quad (\mathrm{mod}\:p)\]
したがって、$ab$ は平方剰余です。

(2) $a,\;b$ がともに平方非剰余なので
\[(ab)^{\frac{p-1}{2}}\equiv (-1)\cdot (-1)=1\quad (\mathrm{mod}\:p)\]
したがって、$ab$ は平方剰余です。

(3) $a,\;b$ のうち一方が平方剰余、他方が平方非剰余なので
\[(ab)^{\frac{p-1}{2}}\equiv 1\cdot (-1)=-1\quad (\mathrm{mod}\:p)\]
よって、$ab$ は平方非剰余となります。（証明終）