【Excel】確率変数と確率分布

確率変数と確率分布

2 枚の硬貨を 1 回投げる試行において、表の出る枚数を $X$ とおきます。「表が出る」という事象を H,「裏が出る」という事象を T で表すと、試行の結果は次の 4 通りです。
 \[\mathrm{TT,\quad TH,\quad HT,\quad HH}\]
$X=k$ の値をとる確率を $P(k)$ で表すと、
 
① TT のとき $X=0$ であり、その確率は $P(0)=1/4$
② TH, HT のとき $X=1$ であり、その確率は $P(1)=2/4$
③ HH のとき $X=2$ であり、その確率は $P(2)=1/4$
 
となります。$X$ と $P(X)$ を表にまとめると次のようになります。
 

一般に $X$ が
 \[x_1,\quad x_1,\quad\cdots\quad x_n\]
という値をとり、$X=x_k$ となる確率 $p_k$ が与えられ、
 \[\sum_{k=1}^{n}p_k=p_1+p_2+\:\cdots\:+p_n=1,\quad(p_k\geq 0)\]
の条件を満たすとき、この $X$ を確率変数 (random variable) とよびます。また $p_k$ を確率分布 (probability distribution) といいます。特に $X$ がとびとびの値 $x_k$ をとるときは $X$ を離散変数とよびます。
 

上の表のように、$X$ と $P(X)$ をまとめた表を確率分布表とよびます。また特に
 \[P(X_k=x_k)=\frac{1}{n}\]
となるような確率分布を一様分布といいます。たとえばサイコロを振る試行において、出た目を $X$ で表すことにすれば、
 \[P(X_k=x_k)=\frac{1}{6}\quad (k=1,2,\cdots 6)\]
となるので、確率分布は一様分布です。$X$ は連続的な値をとることもあり、その場合は連続変数とよびます。

【Excel】サイコロをn回振った時の確率分布

1 つのサイコロを $n$ 回続けて振る試行において、出た目の数の最小値を確率変数 $X$ として、$X$ の確率分布を調べてみます。具体的な計算の前に予測を立てておきましょう。最初の 1 回目はどの値も等しい確率 1/6 で最小値となるはずです。2 回以降では 1 が最小値である可能性が最も高く、続いて 2, 3, 4, 5, 6 と目の大きいものほど最小値である可能性は低くなっていくはずです。またサイコロを振る回数を増やすごとに、最小値が 1 である可能性がより高くなっていき、それに応じて他の値 (2 ～ 6) が最小値をとる可能性が低くなっていくはずです。それでは実際に調べてみましょう。

たとえば「最小値が 3 である」ということは、最小値が 3 以上の値 (3, 4, 5, 6 の値) をとる確率から、最小値が 4 以上の値 (4, 5, 6 の値) をとる確率を差し引いた形で表すことができます。
 \[P(X=3)=P(X\geq 3)-P(X\geq 4)\]
一般に「最小値が k である」確率は
 \[P(X=k)=P(X\geq k)-P(X\geq k+1)\quad (k=1,2,\cdots 6)\]
と表せます。また「最小値が 3 以上の値 (3, 4, 5, 6 の値) をとる」確率は
 \[P(X\geq 3)=\left(\frac{4}{6}\right)^n\]
と書くことができます。つまり「最小値が k 以上の値 (3, 4, 5, 6 の値) をとる」確率は
 \[P(X\geq k)=\left(\frac{7-k}{6}\right)^n\]
によって表すことができます。したがって
 \[P(X=k)=\left(\frac{7-k}{6}\right)^n-\left(\frac{6-k}{6}\right)^n\]
となります。$k$ に 1 から 6 までの値を入れてみると
 \[\begin{align*}P(X=1)&=1-\left(\frac{5}{6}\right)^n\\[6pt]P(X=2)&=\left(\frac{5}{6}\right)^n-\left(\frac{2}{3}\right)^n\\[6pt]P(X=3)&=\left(\frac{2}{3}\right)^n-\left(\frac{1}{2}\right)^n\\[6pt]P(X=4)&=\left(\frac{1}{2}\right)^n-\left(\frac{1}{3}\right)^n\\[6pt]P(X=5)&=\left(\frac{1}{3}\right)^n-\left(\frac{1}{6}\right)^n\\[6pt]P(X=6)&=\left(\frac{1}{6}\right)^n\end{align*}\]
という確率分布が得られます。とはいえ、こんな式を見てもまったくイメージが掴めないので、Excel で様子を見てみましょう。
 

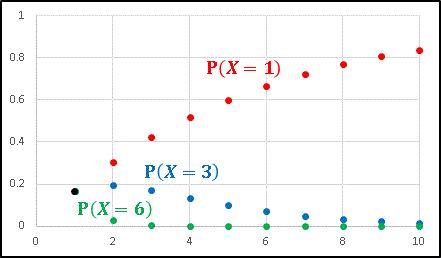
上の図はサイコロを振るごとに $P(X=1),\:P(X=3),\:P(X=6)$ がどのように変化していくかをグラフにしたものです。黒丸は $n=1$ のときで、3 つの点が重なっています（最小値をとる確率が等しくなっています）。予想通り、$P(X=1)$ はその値を急激に伸ばして確率 1 に近づき、反比例して $P(X=3)$ と $P(X=6)$ が値を減らしてその値が 0 に近づいています。もちろん、どの $n$ においても、
 \[P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)+P(X=6)=1\]
という関係が成り立っています。