群数列の練習問題

【SQ22】群数列の第100項までの和

ある規則にしたがって、数字を次のように並べます。
\[1,\:1,\:2,\:1,\:2,\:3,\:1,\:2,\:3,\:4,\:1,\:2,\:3,\:4,\:5,\:\cdots\]
(1) この数列の第 $100$ 項を求めてください。
(2) この数列の初項から第 $100$ 項までの和を求めてください。

【ヒント】群数列 の問題です。第 $100$ 項が第何群に属しているかを考えます。

【考え方】次のような図を描いて問題を視覚化してみると、やるべきことが整理されます。



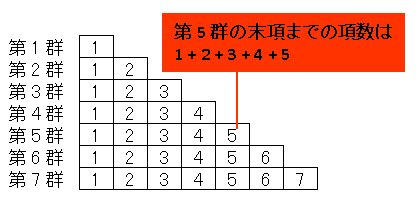
図にあるように、たとえば第 5 群の末項までの項数は
\[1+2+3+4+5=15\]
というように等差数列の和で表されます。また、群の番号は $m$ ではなく、$M$ のような大文字で表すと紛れがなくなります。
　
【解答】(1) 与えられた数列を

 第 $1$ 群：$1$
 第 $2$ 群：$1,\:2$
 第 $3$ 群：$1,\:2,\:3$
 第 $4$ 群：$1,\:2,\:3,\:4$
 第 $5$ 群：$1,\:2,\:3,\:4,\:5$

というような群に分けます。第 $M$ 群の末項までの項数は、
\[\sum_{k=1}^{M}k=\frac{M(M+1)}{2}\]
で表せます。$M=13$ のときに
\[\frac{M(M+1)}{2}=\frac{13(13+1)}{2}=91\]
となるので、第 $91$ 項が第 $13$ 群の末項であることがわかります。$M=14$ のときに
\[\frac{M(M+1)}{2}=\frac{14(14+1)}{2}=105\]
となるので、第 $100$ 項は第 $14$ 群にあることがわかります。第 $14$ 群の数字は次のように並びます。



よって、第 $100$ 項は $9$ となります。

(2) 第 $M$ 群に含まれる数字の和は
\[S(M)=\sum_{k=1}^{M}=\frac{M(M+1)}{2}\]
第 $1$ 群から第 $13$ 群までに含まれる数字の和をとると
\[T=\sum_{M=1}^{13}\frac{M(M+1)}{2}=\frac{1}{2}\cdot\frac{13\cdot 14\cdot 15}{3}=455\]
となります。(1) より、第 $14$ 群の初項から $9$ 項までの和は、
\[\frac{9(1+9)}{2}=45\]
となるので、求める答えは $455+45=500$ となります。参考までに Excel で作成した図を下に載せておきます。

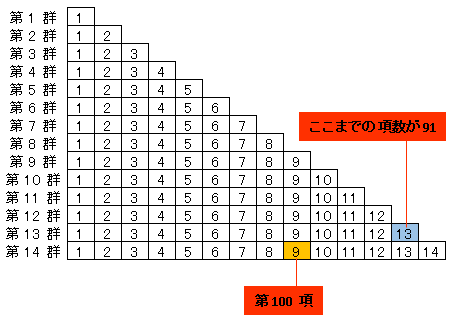
【SQ23】特定の区画に含まれる数の和

数列
\[1,\:2,\:2,\:3,\:3,\:3,\:4,\:4,\:4,\:4,\:5,\:5,\:5,\:5,\:5,\mid 6,\:\cdots,\:\]の第 $n$ 項を $a_n$ とします。この数列を
\[1\mid 2,\:2,\mid 3,\:3,\:3,\mid 4,\:4,\:4,\:4,\mid 5,\:5,\:5,\:5,\:5,\mid 6\:\cdots,\:\]のように、$1$ 個、$2$ 個、$3$ 個 … というように区画にわけます。
(1) $a_{215}$ を求めてください。
(2) 第 $1$ 区画から、第 $20$ 区画に含まれる数の総和を求めてください。
(3) $a_1+a_2+\:\cdots\:+a_n\geq 3000$ を満たす最小の自然数 $n$ を求めてください。
（センター試験　一部改）
【ヒント】今回も群数列の問題です。(2) 第 $n$ 区画には $n$ が $n$ 個ならんでいます。
　
【解答｝数列を区画ごとに整理してみます。

 第 $1$ 区画：$1$
 第 $2$ 区画：$2,\:2$
 第 $3$ 区画：$3,\:3,\:3$
 第 $4$ 区画：$4,\:4,\:4,\:4$
 第 $5$ 区画：$5,\:5,\:5,\:5,\:5$

第 $1$ 区画から第 $M$ 区画までに含まれる項数は、
\[\sum_{k=1}^{M}k=\frac{M(M+1)}{2}\]
となるので、これがおおよそ $215$ になるような、すなわち、
\[M(M+1)\simeq 430\]
となるような $M$ を探します。$400$ の平方根が $20$ なので、$M$ が $20$ 前後の値であることは推測できます。試しに $M=20$ としてみると
\[M(M+1)=20\times 21=420\]
となって少しだけ足りません。$M=21$ とすると
\[M(M+1)=21\times 22=462\]
となるので、$a_{215}$ は第 $21$ 区画にあることがわかります。第 $21$ 区画には $21$ が $21$ 個並んでいるので、$a_{215}=21$ です。

(2) $1^2+2^2+3^2+\:\cdots\:+20^2$ を計算します。
公式 $\displaystyle\sum_{k=1}^{M}k^2=\frac{n(n+1)(2n+1)}{6}$ を用いると
\[S_{20}=\sum_{k=1}^{M}k^2=\frac{20\times 21\times 41}{6}=2870\]
となります。

(3) (2) の結果より、$S_{20}$ にあと少し足せば $3000$ を超えそうだということがわかります。第 $21$ 区画には $21$ が並ぶので、
\[2870+21x\geq 3000\]
を満たすような最小の $x$ を $210$ に加えればよいことになります。
\[x\geq 6.19\]
より、$x=7$ が上の不等式を満たす最小の $x$ です。よって求める答えは $n=217$ です。