円の面積と周長

円周率の定義と近似分数

直径 $d$ の円における周の長さ $L$ とするとき、$L$ と $d$ の比を円周率と定義して、ギリシャ文字 $\pi$ で表します：
\[\pi=\frac{L}{d}\]
すなわち、直径 $1$ をもつ円周の長さが $\pi$ です。$\pi$ の値は円に内接する正多角形の周の長さで近似することができます（正多角形の一辺の長さを小さくするほど近似精度は良くなります）。

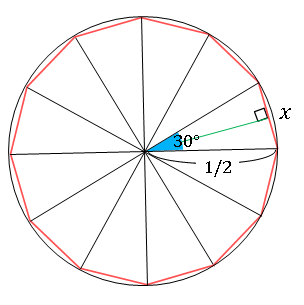
上の図は直径 $1$ の円を正十二角形で近似した例です。正十二角形を分割した一つの辺 $x$ の長さは
\[x=2\times \frac{1}{2}\sin 15^\circ =\sin 15^\circ\]
なので、正十二角形の全周は
\[12x=12\sin 15^\circ \simeq 3.105828541\]
となります。$12$ 角形では精度はよくありませんが、内接する正多角形の辺を小さくしていくことによって
\[\pi=3.141592654\:…\]
という値が得られます。無限級数を用いた精密な円周率の計算法については、グレゴリー級数とマチン級数 を参照してください。

一般に円周や円の面積を計算するときには小数点以下 $2$ 桁までとって、$\pi\simeq 3.14$ が用いられます。連分数展開とよばれる手法を用いると、約率とよばれる近似分数
\[\pi=\frac{22}{7}=3.142857143\:…\]
が得られます。約率より精度の高い近似分数
\[\pi=\frac{355}{113}=3.141592920\:…\]
は密率とよばれ、小数点以下 $6$ 桁まで一致する精度があります。

円周の長さ

一般には円周の長さは直径 $d$ ではなく半径 $r$ を用いて表します。円周率の定義式
\[\pi=\frac{L}{d}\]
において $d=2r$ とおくと、円の周長は
\[L=2\pi r\]
と表されます。半径 $1$ の円の周長は $2\pi$ です。

円の面積

半径 $r$ の円の面積 $S$は
\[S=\pi r^2\]
によって与えられます。初等数学でこの公式を証明することは不可能です（証明には微分積分を用います。記事の最後で解説します）。しかし、直感的な方法で説明することはできます。下図のように半径 $r$ の円を同じ大きさの扇形に切り分けて並べると、平行四辺形のようなものが出来あがります。横の長さは円周 $2\pi r$ の半分、$\pi r$ となっています。円をもっと細かく切り分けて、無限に小さな扇形で分割して組み合わせると、横の長さが $\pi r \times$, 縦の長さが $r$ の長方形になります。

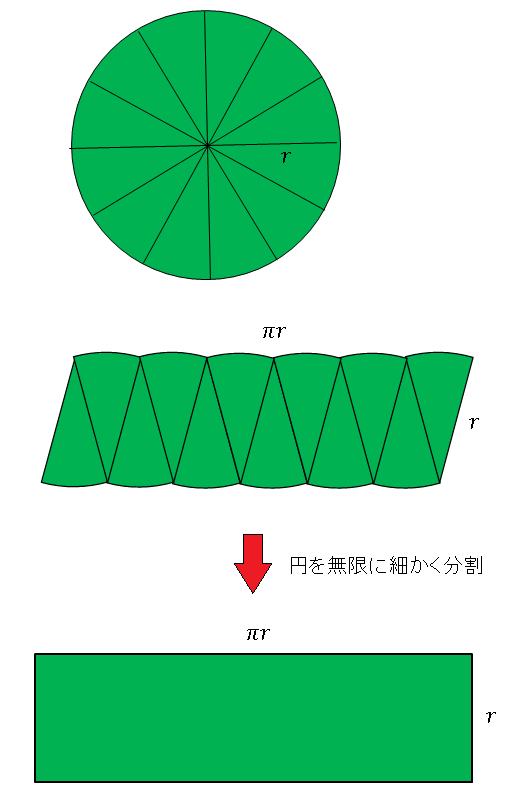
したがって、円の面積は
\[S=r\times \pi r=\pi r^2\]
で与えられます。

半径 $a$ の円の面積を厳密に求めるには、図のような内径 $r$, 幅 $dr$ の細長い同心円を $r$ について $0$ から $a$ まで積分します。


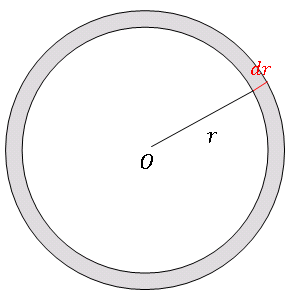
\[\int_{0}^{a}2\pi rdr=2\pi \frac{a^2}{2}=\pi a^2\]