【VBA】台形公式

この記事では台形公式の原理と、VBA による実装、具体的な計算例を解説します。

台形公式

台形公式は関数のグラフと $x$ 軸に囲まれた部分（定積分の値）を台形で埋めて近似計算する方法です。極端に単純化した例として、区間 $[a,\:b]$ において、ある関数 $y=f(x)$ と $x$ 軸に囲まれた面積を次のように 3 つの台形で近似することを考えてみます。

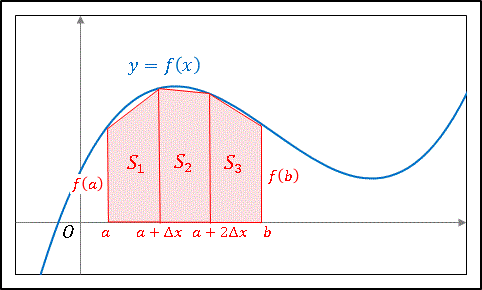
すなわち積分公式で表すと
\[\int_{a}^{b}f(x)dx\simeq S_1+S_2+S_3\]
という近似計算をしようという試みです。区間 $[a,\:b]$ は 3 等分され、1 区分の長さは
\[\Delta x=\frac{b-a}{3}\]
となります。上底と下底の和に高さを掛けて 2 で割ると台形の面積が求められます。左端にある台形の面積 $S_1$ は、$f(a)$ を上底、$f(a+\Delta x)$ を下底として
\[S_1=\frac{1}{2}\left\{ f(a)+f(a+\Delta x) \right\} \Delta x\]
となります。$S_2,\:S_3$ も同様にして
\[\begin{align*}S_2&=\frac{1}{2}\left\{ f(a+\Delta x)+f(a+2\Delta x) \right\} \Delta x\\[6pt]S_3&=\frac{1}{2}\left\{ f(a+2\Delta x)+f(b) \right\} \Delta x\end{align*}\]
これらを全て加えると
\[\begin{align*}S=&S_1+S_2+S_3\\[6pt]&=\frac{1}{2}\left\{ f(a+\Delta x)+f(b) \right\} \Delta x\\[6pt]&+\left\{ f(a+\Delta x)+f(a+2\Delta x) \right\} \Delta x\\[6pt]\end{align*}\]
のように表すことができます。一般的に $n$ 分割した場合を考えてみます。



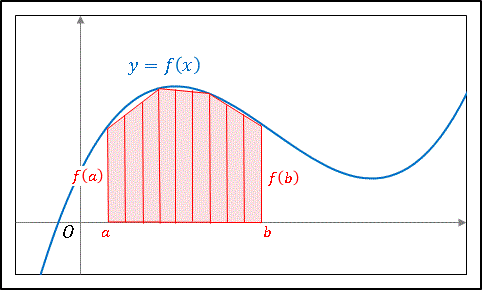
1 区分の長さは
\[\Delta x=\frac{b-a}{n}\]
となり、台形公式による定積分の近似式は
\[\int_{a}^{b}f(x)dx=\frac{b-a}{n}\left\{ \frac{f(a)+f(b)}{2}+\sum_{k=1}^{n-1}f \left( a+k\frac{b-a}{n} \right) \right\}\]
と表されます。

台形公式の実装

台形公式を使って対数関数 $f(x)=\log x$ を任意の区間 $[a,\:b]$ で積分する Function マクロです。あとで真値と比較して、台形公式の近似精度も確認しておきます。

'[VBA]台形公式で対数関数の定積分を計算するFunctionプロシージャ

Function SUMLOG(a As Double, b As Double) As Variant

　　Dim n As Integer, k As Integer
　　Dim delta As Double, sedge As Double, smid As Double

　　'真数条件およびb>aを満たしているかチェックする
　　If a > 0 And b > 0 And b > a Then

　　　　'区間の分割数を指定
　　　　n = 100

　　　　'区分の長さを計算
　　　　delta = (b - a) / n

　　　　'端点における寄与を計算
　　　　sedge = (Log(a) + Log(b)) / 2

　　　　'端点以外の寄与を計算
　　　　For k = 1 To n - 1
　　　　　　smid = smid + Log(a + k * delta)
　　　　Next k

　　　　'台形公式による積分の近似値を得ます
　　　　SUMLOG = (sedge + smid) * delta

　　Else

　　　　SUMLOG = CVErr(xlErrNA)

　　End If

End Funciton

SUMLOG 関数を使うときはセルに

=SUMLOG(a,b)

と入力します。a, b は非負かつ a < b となるように指定しないとエラーが表示されます。

上のマクロで a, b にそれぞれ 1, 10 を指定したとき、すなわち、台形公式で定積分
\[\int_{1}^{10}\log xdx\]
を計算させたときの戻り値と真値を比較すると

 戻り値：14.025　　真値：14.026

となって 4 桁まで一致する精度があります。この精度は分割数 n を大きくすることによって高めることができます。上のマクロで n = 1000 と書き換えてみると

 戻り値：14.0258　　真値：14.0259

というように 5 桁の精度となります。

INTEGRAL関数

次は $x$ と $y$ のデータをまとめて指定して定積分を計算する INTEGRAL 関数を作ってみます。INTEGRAL関数は配列を使ったユーザー定義関数です。

'[VBA]台形公式による定積分関数

Function INTEGRAL(xy As Range) As Double　　Dim i As Integer, u As Integer

　　Dim a As Double, b As Double
　　Dim h As Double, s As Double
　　Dim mydata As Variant

　　'xyを2次元配列変数に変換
　　mydata = xy

　　'配列の要素数
　　u = UBound(mydata, 1)

　　'台形公式の適用
　　For i = 1 To u - 1
　　　　h = mydata(i + 1, 1) - mydata(i, 1)
　　　　s = s + (mydata(i, 2) + mydata(i + 1, 2)) * h / 2
　　Next i

　　INTEGRAL = s

End Function

この関数は実践的なデータを想定して作成しました。ワークシートにデータが用意されていれば、関数を具体的な形 $y=f(x)$ で表せなくても積分を実行できます。とはいえ、あまり凸凹したデータだと精度が悪くなるので、ある程度の滑らかさは必要です。下の図は二次関数データを $x=-1$ から $x=1$ まで用意して、INTEGRAL関数で積分の近似値を求めています。

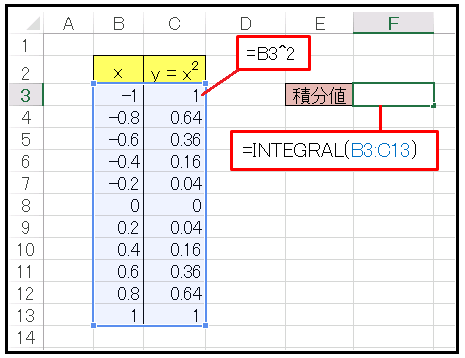
台形近似を使用しますが、普通の台形近似公式とは少し異なり、セルに入力された区間ごとに近似を行なっています。上の例では $x$ は一定間隔で入力されていますが、所々で刻み幅が変わってもかまいません。具体的には一番左端の台形は
\[S(1)=\frac{1}{2}(1^2+0.64^2)\{-0.8-(-1)\}=0.164\]
と計算されます。同様に全ての行について台形の面積を求めて、それを全部足し合わせて積分の近似値とします。この関数を使うときはセルに

=INTEGRAL(範囲)

と入力します。範囲は 2 列まとめて指定してください。上の例では

=INTEGRAL(B3:C13)

と入力して 0.68 という値が返ります。真値は 0.67 です。刻み幅を細かくするほど精度は上がります。上の例では $x$ を 0.2 刻みとしていますが、0.1 刻みでデータを入力すると、0.67 という値が返ります。

もう１つ計算例を載せておきます。分数関数 $y=1/x$ を $x=1$ から $x=2$ まで積分してみます。



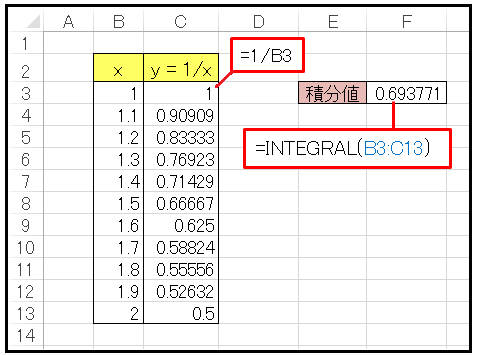
上のようなシートを作って、F3 セルに

=INTEGRAL(B3:C13)

と入力すると 0.694 の値が返ります。真値は $\ln2=0.693$ なので、かなり良い精度だと思います。

【補足】台形の面積

台形の面積の求め方を確認しておきましょう。上底の長さ $a$、下底の長さが $b$、高さ $h$ の台形の面積を求める公式は
\[S=\frac{(a+b)h}{2}\]
で与えられます。$h$ が明示されていなくても、一方の脚の長さ $c$ と、脚と下底のなす角度 $\theta$ がわかっている場合、高さ $h$ は
\[h=c\sin\theta\]
と表せるので、台形の面積は
\[S=\frac{(a+b)c\sin\theta}{2}\]
のようにして求めることができます。