区間縮小法とボルツァノ-ワイエルシュトラスの定理

この記事では区間縮小法を証明し、そこから有界な数列が収束する部分列をもつこと（ボルツァノ-ワイエルシュトラスの定理）を導きます。

区間縮小法

次のような数列 $a_n,\:b_n$ を考えてみます。
 \[a_n=1-\frac{1}{n},\quad b_n=1+\frac{1}{n}\]
$a_n$ は 0 から 1 に、$b_n$ は 2 から 1 に近づいていく数列です。
 

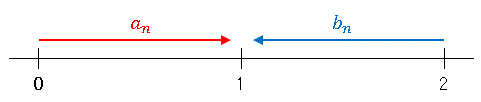
上図では $a_n$ は左から、$b_n$ は右から 1 へ収束して等しい値になります。このような 1 が存在するということを主張するのが区間縮小法です。一般的な定理を書くと、

【区間縮小法の証明】有界な単調増加（単調減少）数列は上限（下限）に収束する ので、
 \[\lim_{n\rightarrow \infty}a_n=a,\quad \lim_{n\rightarrow \infty}b_n=b\]
となるような $a,\:b$ が存在することは明らかです。また数列についての基本的な定理によると、2 つの数列 $\{a_n\}$ と $\{b_n\}$ が
 \[\lim_{n\rightarrow \infty}a_n=a,\quad \lim_{n\rightarrow \infty}b_n=b\]
を満たし、かつ十分に大きな数 $n$ に対して $a_n \geq b_n$ が成立するならば、$a\geq b$ が成り立つので、
 \[a_n\leq a\leq b \leq b_n\]
が得られます。したがってすべての $n$ について
 \[|b_n-a_n|\geq |b-a|\geq 0\]
が成り立ちます。数列 $\{a_n\}$ と $\{b_n\}$ は
 \[\lim_{n\rightarrow \infty}(b_n-a_n)=0\]
を満たすものとしているので、$a=b$ が成立します。

ボルツァノ-ワイエルシュトラスの定理

1 つの数列 $\{a_n\}$ から無限個の項を抜き出して、順序は変えないように新しい数列 $\{b_n\}$ をつくります。このとき $\{b_n\}$ は $\{a_n\}$ の部分列であるといいます。たとえば
 \[a_1,\:a_2,\:a_3,\:a_4,\:a_5,\:a_6,\:a_7,\:\cdots\]
があって、$n$ が奇数のところを抜き出してそのままの順に並べると
 \[b_1,\:b_3,\:b_5,\:b_7,\:b_9,\:b_{11},\:b_{13},\:\cdots\]
となって無限に続く数列となり、$\{b_n\}$ は $\{a_n\}$ の部分列となっていることがわかります。このようにすればどのような $\{a_n\}$ も部分列をもつことになりますが、今調べたいのは有界な数列の中に、収束するような部分列が含まれているかどうかということです。そこで少し複雑な振る舞いをする次のような数列 $\{a_n\}$ を考えてみます。
 \[a_n=1-\frac{(-1)^n}{n}\]
各項を具体的に書き並べてみると
 \[2,\:\frac{1}{2},\:\frac{4}{3},\:\frac{3}{4},\:\frac{4}{5},\:\cdots\]
となります。この数列は 1 を交互にまたぎながら次第に 1 へと近づいていきます。直感的には下図のように 1 を含む適当な区間をとって、その中にある数列を $\{b_n\}$ とすれば収束する部分列となるのは明らかに思えます。
 

しかし後の証明の理解のためにもう少し丁寧に部分列を作ってみましょう。
下図のように区間を次々と半分にしていって、その中にある $\{a_n\}$ から 1 つずつ選んで $b_1,\:b_2,\:b_3,\cdots$ としていきます。
 

このようにすることで $\{b_n\}$ の各項には大きさに制限がつき、
 \[\begin{align*}&0\lt b_1\leq 2\\[6pt]&1\leq b_2\leq 2\\[6pt]&1\leq b_3\leq 3/2\\[6pt]&1\leq b_4\leq 5/4\end{align*}\]
というように、どんどん範囲を狭めていくことができます。区間はいくらでも小さくなっていくので $\{b_n\}$ が 1 に収束することがわかります。以上のことを一般化した定理とその証明を載せておきます。

【ボルツァノ – ワイエルシュトラスの定理の証明】
数列 $\{a_n\}$ は有界なので、$\{a_n\}$ を全て含むような区間 $[p_0,\:q_0]$ が存在するはずです。この区間 $[p_0,\:q_0]$ を 2 等分して無数の $\{a_n\}$ を含んでいるほうの区間を $[p_1,\:q_1]$ とします。もし両方の区間がともに無数の $\{a_n\}$ を含んでいるのなら、（どちらでもいいのですが）とりあえず右側の区間を $[p_1,\:q_1]$ と定めることにしておきます。そしてまた $[p_1,\:q_1]$ を 2 等分して区間 $[p_2,\:q_2]$ を作ります。$[p_n,\:q_n]$ の区間の長さは
 \[\frac{1}{2^n}(q_0-p_0)\]
となります。また明らかに
 \[p_0\leq p_1\leq\cdots\leq p_n\leq\cdots\leq q_n\leq\cdots\leq q_1\leq q_0 \]
が成り立ちます。よって アルキメデスの原理 より
 \[\lim_{n\rightarrow \infty}\frac{1}{2^n}=0\]
となるので、
 \[\lim_{n\rightarrow \infty}(q_n-p_n)=\lim_{n\rightarrow \infty}\frac{1}{2^n}(q_0-p_0)=0\]
が成り立ち、すると区間縮小法から
 \[\lim_{n\rightarrow \infty}p_n=\lim_{n\rightarrow \infty}q_n=a\]
となる実数 $a$ が存在することになります。次に区間
 \[[p_0,\:q_0],\:[p_1,\:q_2],\:\cdots\:[p_n,\:q_n],\:\cdots\]
から 1 つずつ $a_n$ を取り出し、あらためて
 \[b_1,\:b_2,\:b_3,\:\cdots\:b_n,\:\cdots\]
という数列をつくると、
 \[p_k\leq b_k\leq q_k\]
が成り立っています。$k\rightarrow \infty$ とすると「はさみうちの原理」より
 \[\lim_{n\rightarrow \infty}b_k=a\]
となって、部分列 $\{b_k\}$ は $a$ に収束することがわかります。