二項分布
成功率 $p$ の試行を $n$ 回繰り返して $k$ 回成功する確率は
\[p_r={}_n\mathrm{C}_k\:p^k(1-p)^{n-k}\]
によって与えられます (『反復試行』の記事参照)。そこでたとえば 1 枚の硬貨を 5 回投げて表が出る回数を $X$ として、$X=k$ となる(つまり $k$ 回表が出る)確率は
\[P(X=k)={}_5\mathrm{C}_k\left(\frac{1}{2}\right)^k\left(\frac{1}{2}\right)^{5-k}={}_5\mathrm{C}_k\left(\frac{1}{2}\right)^5\]
となります。すべての $k$ について具体的に書き並べてみると以下のようになります。
\[\begin{align*}P(X=0)={}_5\mathrm{C}_0\left(\frac{1}{2}\right)^5=\frac{1}{32}\\[6pt]P(X=1)={}_5\mathrm{C}_1\left(\frac{1}{2}\right)^5=\frac{5}{32}\\[6pt]P(X=2)={}_5\mathrm{C}_2\left(\frac{1}{2}\right)^5=\frac{10}{32}\\[6pt]P(X=3)={}_5\mathrm{C}_3\left(\frac{1}{2}\right)^5=\frac{10}{32}\\[6pt]P(X=4)={}_5\mathrm{C}_4\left(\frac{1}{2}\right)^5=\frac{5}{32}\\[6pt]P(X=5)={}_5\mathrm{C}_5\left(\frac{1}{2}\right)^5=\frac{1}{32}\end{align*}\]
実際にコインを投げるところを想像すると、この結果は直感と合っています。全てが裏である (X=0) 、あるいは表である(X=5)確率はとても小さく、表が 2 枚と 3 枚である確率が最も大きくなっています。また各試行において「表が出る」確率と「裏が出る」確率は同じなので、
\[P(X=0)=P(X=5)\\[6pt]P(X=1)=P(X=4)\\[6pt]P(X=2)=P(X=3)\]
というように対称形になっています。一般に確率変数のとり得る値が正の整数であり、確率密度関数が次のような形(ただし $p+q=1$)
\[f(x)=\begin{cases}\displaystyle {}_n\mathrm{C}_xp^xq^{n-x} & (x=0,1,2,\cdots,n)\\[6pt]0 & (x\neq 0,1,2,\cdots,k)\end{cases}\]
で与えられるような確率分布を 二項分布(Binomial Distribution)あるいはベルヌーイ分布(Bernoulli distribution) とよび、$B(n,p)$ で表します。試行回数と 1 回ごとの確率が与えられると分布が決まるということです。
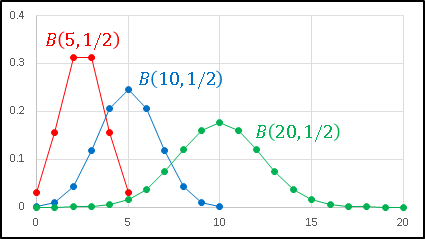
上のグラフは硬貨を 5 回(赤)、10 回 (青)、20 回投げて表(あるいは裏)が何回出るかという確率を示す分布図です。試行回数 $n$ が増えると極大値が右方向へずれて裾野が広がっていきます。$n/2$ が平均値(期待値)であり、$n$ の増加にともなって平均値とその周辺値との確率の差が小さくなっていく傾向があります。つまり硬貨を 20 回投げたとき、表が 10 枚出る確率も、9 枚出る確率も、それほど差はないということです。
二項分布の期待値
二項分布の確率の和が 1 になっていることを確認しておきましょう。確率密度関数
\[f(x)={}_n\mathrm{C}_xp^xq^{n-x}\quad (x=0,1,2,\cdots,n)\tag{1}\]
において $x=0$ から $x=n$ の和をとると
\[\sum_{x=0}^{n}f(x)={}_n\mathrm{C}_0q^n+{}_n\mathrm{C}_1pq^{n-1}+\cdots+{}_n\mathrm{C}_np^n\tag{2}\]
となりますが、左辺は $(p+q)^n$ の展開式(二項展開)に他なりません(ですから二項分布という名称なのです)。$p+q=1$ なので
\[\sum_{x=0}^{n}f(x)=1\tag{3}\]
となって確率の和が 1 であるという条件を満たしていることがわかります。次は二項分布の平均値(期待値)を求めてみます。やや技巧的ですが
\[\sum_{x=0}^{n}{}_n\mathrm{C}_xp^xq^{n-x}=(p+q)^n\tag{4}\]
の両辺を $p$ で微分すると
\[\sum_{x=0}^{n}x{}_n\mathrm{C}_xp^{x-1}q^{n-x}=n(p+q)^{n-1}\tag{5}\]
両辺に $p$ を掛けて $p+q=1$ を用いると
\[\sum_{x=0}^{n}x{}_n\mathrm{C}_xp^xq^{n-x}=np\tag{6}\]
という式が得られます。ここで右辺は
\[\sum_{x=0}^{n}x{}_n\mathrm{C}_xp^xq^{n-x}=\sum_{x=0}^{n}f(x)\tag{7}\]
なので、これは平均値 $\mu$ です。よって
\[\mu=E(X)=np\tag{A}\]
というように平均値は試行回数と確率の積で表されます。たとえばコイン投げのように確率 1/2 の試行を 100 回繰り返せば、表も裏もおおよそ 50 回ずつ出るという、当たり前のことを式にしているだけです。
二項分布の分散
次は二項分布の分散を求めます。(5) 式を再掲すると
\[\sum_{x=0}^{n}x{}_n\mathrm{C}_xp^{x-1}q^{n-x}=n(p+q)^{n-1}\]
この式をもう一度 $p$ で微分します。
\[\sum_{x=0}^{n}x(x-1){}_n\mathrm{C}_xp^{x-2}q^{n-x}=n(n-1)(p+q)^{n-1}\tag{8}\]
両辺に $p^2$ をかけて $p+q=1$ を用いると
\[\sum_{x=0}^{n}x(x-1){}_n\mathrm{C}_xp^{x}q^{n-x}=n(n-1)p^2\tag{9}\]
となります。ここで (6) 式
\[\sum_{x=0}^{n}x{}_n\mathrm{C}_xp^xq^{n-x}=np\]
を用いると
\[\sum_{x=0}^{n}x^2{}_n\mathrm{C}_xp^{x}q^{n-x}=n(n-1)p^2+np\tag{10}\]
となります。ここで分散の公式 $\sigma^2=E(X^2)-\mu^2$ を
\[\begin{align*}\sigma^2&=\sum_{x=0}^{n}x^2f(x)-\mu^2\\[6pt]&=\sum_{x=0}^{n}x^2{}_n\mathrm{C}_xp^{x}q^{n-x}-\mu^2\end{align*}\]
と書いてみると、$\mu=np$ および (9) 式
\[\sum_{x=0}^{n}x(x-1){}_n\mathrm{C}_xp^{x}q^{n-x}=n(n-1)p^2\]
を用いて二項分布の分散
\[\sigma^2=np(1-p)\tag{B}\]
を得ます。分散も試行回数 $n$ に比例して分布の幅が広がります。
硬貨を 10 回投げて表が出る回数を $X$ とすると、$n=10,\:p=1/2$ なので、その分散は
\[\sigma^2=10\cdot 0.5(1-0.5)=2.5\]
で与えられます。また標準偏差は
\[\sigma=\sqrt{2.5}=1.581\]
となります。
【Excel】BINOM.DIST関数
二項分布を調べるために、Excel には BINOM.DIST という関数が用意されています。BINOM.DIST は BINOMIAL DISTRIBUTION (二項分布) の略です。この関数は
=BINOM.DIST(X,n,p,0)
という形で使用します。すなわち
=BINOM.DIST(成功数,試行回数,成功率,関数形式)
であり、引数に応じて確率 P(X) を返します。関数形式は 0 としておいてください( 1 と指定すると累積分布関数になります)。たとえば、
=BINOM.DIST(2,10,1/6,0)
と入力すると「サイコロを 10 回振って 1 の目が 2 回出る確率」に相当する値を計算します。この関数を用いて X を横軸に、P(X) を縦軸にプロットしてみましょう。まずはワークシートに次のようなデータを作っておきます。
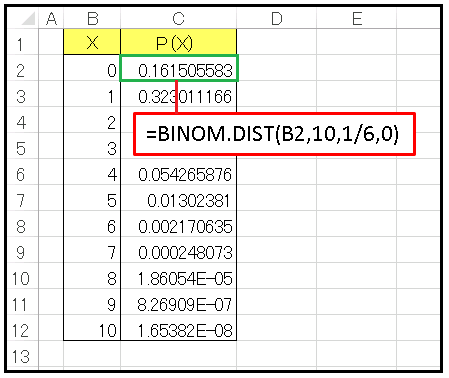
B 列には X の値を 0 から 10 までを入れておきます。セル C2 には
=BINOM.DIST(B2,10,1/6,0)
と入力し、オートフィルで(あるいはセルの右下隅をダブルクリックして)セル C12 までデータを埋めます。これをマーカー付散布図でプロットしてみると、次のようなグラフが得られます。
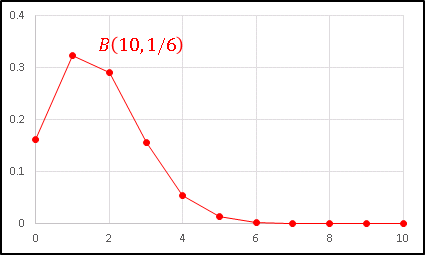
これが二項分布 B(10, 1/6) にしたがう確率密度のグラフです。「1 の目が 1 回だけ出る確率」が最も高く、その次に「2 回出る確率」となっています。二項分布の平均値は μ = np で計算できることが知られています。今の場合は
μ = 10/6 = 5/3 = 1.667
となり、1 と 2 の中間あたりに平均値が存在していることになります。要するにサイコロを 10 回投げると「1 回か 2 回ほど 1 の目が出る」ということです。グラフを見ると、6 回以上同じ目が出るのは極めて稀な現象であることもわかります。
二項分布 B(n, p) が p に応じてどのように変化するのか調べてみましょう。先ほどのグラフに B(10, 5/6) と B(10, 3/6) のグラフを重ねてみます。
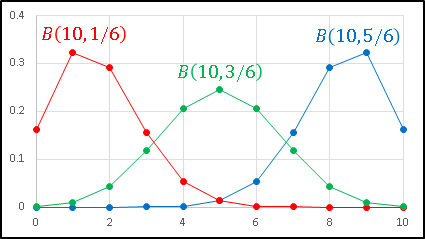
青い線で描かれた B(10, 5/6) は B(10, 1/6) と対称な形になっています。p = 5/6 は「 1 以外の数が出る確率」、言い換えると「 1 の目が 1 回も出ない」確率に相当するからです。また緑の線で描かれた B(10, 3/6) すなわち B(10, 1/2) は「コインを 10 回投げて表が X 回出る」ような確率分布です。たとえば「表が 4 回出る確率」と「表が 6 回出る確率 = 裏が 4 回出る確率」は同じなので、このように左右対称なグラフになります。

エクセルや数学に関するコメントをお寄せください