【Excel】罫線で数直線を作成します
オートシェイプ(図形挿入機能)を使わずに罫線 (けいせん)だけで数直線を作成する方法を紹介します。Excel で数直線を描きたいという需要が世間にどれぐらいあるのか知りませんが(おそらくほとんどない)、もし興味があれば読んでください。基本的な罫線の引き方は知っているという前提でお話します。
セルの縦幅と横幅を適当に調整しておいてから、下の図のように長い罫線を横に1本引いて、縦には2セル間隔で罫線を引いておきます。縦線は数直線の目盛になります。
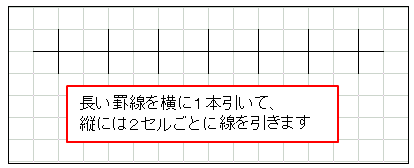
次に数直線の下のセルを目盛が中央にくるように 2 つごとに結合します( [ホーム] タブの [セルを結合して中央揃え] をクリックします)。
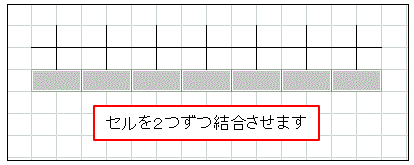
結合したセルに目盛の値を入力します。
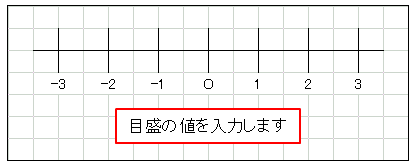
最後に行の高さを小さく (おおよそ 4 ポイントぐらいに) 設定して、数直線の完成です。
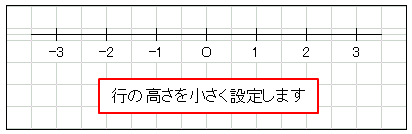
数直線の作図を図形挿入機能でやろうとすると、目盛の長さの調節などが本当に面倒なので、やっぱり罫線機能が便利です。

エクセルや数学に関するコメントをお寄せください
ちょうどいいワークシートが見つからなくて,困っていました。
教えていただいたやり方で,1000までの数の数直線ができました!ありがとうございます!
お役に立てて何よりです。
…… でも、そんなに長い数直線をどのような目的で作成されたのか、とても気になります。