補充法則と相互法則

定理 F11 を再掲します。

一般の正負の整数 $n$ は、$q_1,\:q_2,\:,\cdots$ を奇素数、$s,\:t_1,\:t_2,\:\cdots$ を $0$ 以上の整数として
\[n=\pm\,2^sq_1^{t_1}q_2^{t_2}\cdots\]
のように表せるので、整数が平方剰余であるかどうかは

\[\left(\frac{n}{p}\right)=\left(\frac{-1}{p}\right)\left(\frac{2}{p}\right)^s\left(\frac{q_1}{p}\right)^{t_1}\left(\frac{q_2}{p}\right)^{t_2}\cdots\]
を計算して判定することができます。すなわち任意の整数について、素因数分解によって奇素因数 $q_i$ をすべて求めて
\[\left(\frac{-1}{p}\right),\:\left(\frac{2}{p}\right),\:\left(\frac{q_i}{p}\right)\]
を計算すれば、その整数の平方剰余／平方非剰余を判定することができるということです。

第１補充法則

$\displaystyle\left(\frac{-1}{p}\right)$ は前々回記事で扱ったオイラーの判定条件

において $a=-1$ とすればよいだけで、平方剰余の第１補充法則とよばれています：

ここで $p$ を $4$ で割ったときの余り ($\mathrm{mod}\:4$) で分類すると、$p=4k+1$ あるいは $p=4k+3$ のいずれかになります（$4k$ や $4k+2$ は偶数なので $p$ として不適）。それぞれの場合について上の第１補充法則に入れて計算してみると、
\[\left(\frac{-1}{p}\right)= (-1)^{2k}=1,\quad \left(\frac{-1}{p}\right)= (-1)^{2k+1}=-1\]
となるので、
\[x^2\equiv -1\quad (\mathrm{mod}\:p)\]
が解をもつのは、$p=4k+1$ の形の素数のときだけです。たとえば、
\[x^2\equiv -1\quad (\mathrm{mod}\:5)\]
すなわち
\[x^2\equiv 4\quad (\mathrm{mod}\:5)\]
は解をもつということです。実際に確認してみましょう。
\[1^2,\:2^2,\:3^2,\:4^2,\:5^2\]
を $5$ で割ってみると
\[1,\:4,\:,\:4,\:1,\:0\]
となって、確かに余り $4$ が現れています。すなわち
\[x\equiv 2,\:3\quad (\mathrm{mod}\:5)\]
が解となります。

第２補充法則

次は $a=2$ の場合です。これもオイラーの判定条件に当てはめて
\[\left(\frac{2}{p}\right)\equiv 2^{\frac{p-1}{2}}\quad (\mathrm{mod}\:p)\]
によって判定することもできますが、たとえば $p=17$ とすると
\[\left(\frac{2}{11}\right)\equiv 2^8\quad (\mathrm{mod}\:17)\]
を計算しなくてはならず、少し面倒です。右辺が $(-1)^t$ の形になっていれば、$t$ の偶奇によってすぐに平方剰余／非剰余を判定できます。そこで登場するのが次の平方剰余の第２補充法則です。

この定理の証明の準備として、前回記事で扱った ガウスの補題 を少し噛み砕いた表現に直しておきます（意味は同じです）。

さらに $a=2$ とすると、$(2,\:p)=1$ なので

第２補充法則の証明にはこの定理を用いますが、一般的な証明は少し難しいので、まずは $p=11$ として具体的に調べてみます。
\[2,\:4,\:6,\:8,\:10\]
を $11$ で割って余りを並べると、
\[2,\:4,\:6,\:8,\:10\tag{1}\]
というように同じ数が並びます。このなかに $p/2=5.5$ より大きな数は $3$ 個あるので、ガウスの補題により
\[\left(\frac{2}{11}\right)=(-1)^3=-1\]
となって、$x^2\equiv 2\:(\mathrm{mod}\:11)$ が解をもたないことがすぐにわかります。しかし後の一般的証明のために、この $t=3$ を別の方法で数えてみます。(1) になかで $p/2=5.5$ より大きな余りは
\[6,\:8,\:10\tag{2}\]
です。これらの数を $11$ から引くと
\[5,\:3,\:1\tag{3}\]
というように $5.5$ より小さな奇数が並びます。つまり $p/2=5.5$ より大きな数の個数は $5.5$ より小さな奇数の個数に等しくなります。これは
\[t\equiv 1+3+5\quad (\mathrm{mod}\:2)\]
のように表すこともできます。$\mathrm{mod}\:2$ で考えているので、これに偶数をいくつ足しても合同ですから、
\[t\equiv 1+2+3+4+5\quad (\mathrm{mod}\:2)\]
と書き換えることもできます。以上を踏まえて一般的な証明を記述します。

[定理F14の証明]
$2,\:4,\:6,\:\cdots,\:p-2,\:p-1$ を $11$ で割って余りを並べると、
\[2,\:4,\:6,\:\cdots,\:p-2,\:p-1\tag{4}\]
となります。このなかに $p/2$ より大きな数 $r$ が $t$ 個あると仮定します。$r$ は偶数なので $p-r$ は奇数です。$r\gt p/2$ なので、
\[p-r\lt\frac{p}{2}\]
となります。つまり $t$ は $p/2$ より小さな奇数の個数と一致するので
\[t\equiv 1+3+5+\cdots +\frac{p-1}{2}\quad (\mathrm{mod}\:2)\]
これに偶数をいくつ加えても合同なので、等差級数の公式を用いて
\[\begin{align*}t\equiv& 1+2+3+4+5+\cdots +\frac{p-1}{2}\\[6pt]
\equiv& \frac{1}{2}\,\frac{p-1}{2}\left(1+\frac{p-1}{2}\right)=\frac{p^2-1}{8}\quad (\mathrm{mod}\:2)\end{align*}\]
が得られます（証明終）。

相互法則（Reciprocity Law）

　次は相互法則（reciprocity law） の証明を行ないます。

相互法則はオイラーによって予想され、ガウスによって証明されました。
この定理は $\mathrm{mod}\:p$ と $\mathrm{mod}\:q$ の世界を結びつけるもので、初等整数論の到達点であり、近代数論の土台となる重要定理といわれています。

証明には ガウスの補題 を用います：

ガウスの補題において $a=q$ とおくと、
\[qx\quad \left(x=1,\:2,\:\cdots,\:\frac{p-1}{2}\right)\]
を $p$ で割ったときの余りを並べたときに、$p/2$ より大きいものが $n$ 個あるならば
\[\left(\frac{q}{p}\right)=(-1)^n\]
が成り立ちます。同様に、
\[py\quad \left(y=1,\:2,\:\cdots,\:\frac{q-1}{2}\right)\]
を $q$ で割ったときの余りを並べたときに、$q/2$ より大きいものが $m$ 個あるとすれば
\[\left(\frac{p}{q}\right)=(-1)^m\]
が成り立ちます。すなわち
\[\left(\frac{q}{p}\right)\left(\frac{p}{q}\right)=(-1)^n (-1)^m=(-1)^{m+n}\]
なので、
\[m+n\equiv \left(\frac{p-1}{2}\right)\left(\frac{q-1}{2}\right)\quad (\mathrm{mod}\:2)\tag{R1}\]
が成り立つ（両辺の偶奇が一致する）ことを示せれば、相互法則
\[\left(\frac{q}{p}\right)\left(\frac{p}{q}\right) =(-1)^{\frac{p-1}{2}\frac{q-1}{2}}\tag{R2}\]
を証明できたことになります。

[R1の証明] 格子点を使って証明します。



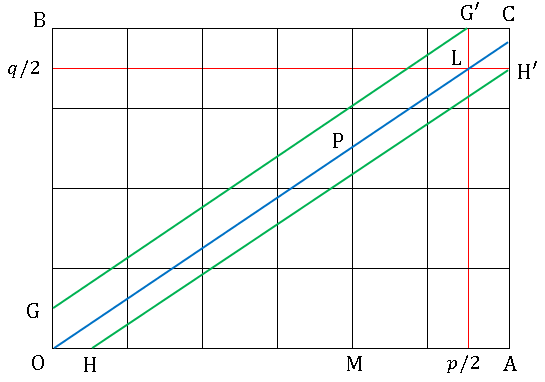
$\displaystyle\left(\frac{p+1}{2},\:\frac{q+1}{2}\right)$ を点 $\mathrm{C}$ として、$\mathrm{ABCD}$ の内側に格子点を打ち、原点 $\mathrm{O}$ と $\mathrm{L}(p/2,\:q/2)$ を結ぶ直線を引きます。直線 $\mathrm{OL}$ の方程式は
\[y=\frac{qx}{p}\]
です。また、直線 $\mathrm{OL}$ を $y$ 軸方向と $x$ 軸方向に $1/2$ だけ平行移動させた直線をそれぞれ $\mathrm{GG’},\:\mathrm{HH’}$ とします。$qx$ を $p$ で割ったときの余りを $r$ とすると
\[qx=py+r\]
と表せます。この式を変形すると
\[\frac{qx}{p}=p+\frac{r}{p}\]
となります。$r$ が $p/2$ より大きいということは、
\[\frac{r}{p}\gt \frac{1}{2}\]
すなわち $qx/p$ の小数部分が $1/2$ よりも大きいことを意味します。

これを図で考えると、$\mathrm{P}$ は直線 $\mathrm{MP}$ 上で、$\mathrm{P}$ を挟む $2$ つの格子点の間の半分より上にあることになります。言い換えると、$\mathrm{P}$ から縦に最も近い格子点は $\mathrm{OL}$ より上側のほうだということです。つまり $n$ は平行四辺形 $\mathrm{OGG’L}$ の内側にある格子点ということになります。

同様に $m$ は平行四辺形 $\mathrm{OHH’L}$ の内側にある格子点です。角にある小さな三角形も加えても格子点の数は変わらないので、$m+n$ は六角形 $OGG’CH’H$ の内部にある格子点の数に等しいことになります。

ここで $\mathrm{OC}$ の中点 $\displaystyle\left(\frac{p+1}{4},\:\frac{q+1}{4}\right)$ は六角形の対称の中心で、格子点はこの点に関して $2$ つずつ対称に存在していることになります。つまり、$m+n$ が偶数か奇数であるかは、$\displaystyle\left(\frac{p+1}{4},\:\frac{q+1}{4}\right)$ 自身が含まれるかどうかで決まります（含まれるなら奇数、含まれないなら偶数です）。含まれるときは、$s,\:t$ を整数として
\[\frac{p+1}{4}=s,\quad\frac{q+1}{4}=t\]
これを少し変形して
\[\frac{p-1}{2}=2s-1,\quad\frac{q-1}{2}=2t-1\]
となります。すなわち $m+n$ が奇数であるということは $\displaystyle\left(\frac{p-1}{2},\:\frac{q-1}{2}\right)$ がともに奇数であることと同じです。したがって
\[m+n\equiv \left(\frac{p-1}{2}\right)\left(\frac{q-1}{2}\right)\quad (\mathrm{mod}\:2)\tag{R1}\]
が成り立つことがわかり、これによって平方剰余の相互法則

\[\left(\frac{q}{p}\right)\left(\frac{p}{q}\right) =(-1)^{\frac{p-1}{2}\frac{q-1}{2}}\tag{R2}\]
が示されました。

mod 4 による判定

奇数を $4$ で割ったときの余りは $1$ か $3$ のどちらかです。すなわち

となります。$x\equiv 1\quad (\mathrm{mod}\:4)$ のときは
\[\frac{x-1}{2}=\frac{4k+1-1}{2}=2k\]
であり、$x\equiv 3\quad (\mathrm{mod}\:4)$ のときは
\[\frac{x-1}{2}=\frac{4k+3-1}{2}=2k+1\]
となります。したがって、$p\equiv 1$ または $q\equiv 1\:(\mathrm{mod}\:4)$ のときは $\displaystyle\frac{p-1}{2}\frac{q-1}{2}$ は偶数、$p\equiv 3$ かつ $q\equiv 3\:(\mathrm{mod}\:4)$ のときは $\displaystyle\frac{p-1}{2}\frac{q-1}{2}$ は奇数となります。これを使って相互法則を書き直しておきます。

平方剰余の例題

これまでに得た知識を総合すると、どのような方程式についても、平方剰余／非剰余の判定ができます（もちろん $a$ や $p$ があまりに大きな値であれば計算は大変です）。判定に必要となる定理をすべて再掲します。

それでは合同方程式
\[x^2\equiv 18\quad (\mathrm{mod}\:31)\]
に解があるかどうかを調べましょう（このような簡素な問いに答えるために、私たちはここまで頑張ってきたのです！）。ルジャンドル記号を用いて表すと
\[\left(\frac{18}{31}\right)\]
の値が $1$ なら解があり（平方剰余であり）、$-1$ なら解なし（平方非剰余）です。まずは積の形に分解します。
\[\left(\frac{18}{31}\right)=\left(\frac{2\cdot 3^2}{31}\right)=\left(\frac{2}{31}\right)\left(\frac{3}{31}\right)^2\]
$\displaystyle\left(\frac{2}{31}\right)$ は第２補充法則によって計算できます。
\[\left(\frac{2}{31}\right)=(-1)^{\frac{31^2-1}{8}}=1\]
$\displaystyle\left(\frac{3}{31}\right)$ の計算には相互法則を用います。相互法則によれば
\[\left(\frac{3}{31}\right)\left(\frac{31}{3}\right)=(-1)^{\frac{3-1}{2}}(-1)^{\frac{31-1}{2}}=1\]
なので、
\[\left(\frac{3}{31}\right)=\left(\frac{31}{3}\right)\]
と書き直せます。このように変形できることが相互法則の恩恵なのです。なぜなら、$31$ は $\mathrm{mod}\:3$ において $1$ と合同なので、
\[\left(\frac{31}{3}\right)=\left(\frac{1}{3}\right)=1\]
と計算できます (任意の $p$ で、$x^2\equiv 1$ は解をもちます)。したがって、
\[\left(\frac{18}{31}\right)=1\]
となり、$x^2\equiv18\:(\mathrm{mod}\:31)$ は解をもつことがわかりました。すなわち $18$ は $31$ の平方剰余です。

Excelで平方剰余の問題を解いてみます

コンピュータの力を借りると、平方剰余／非剰余の判定のみならず、実際の解を求めることも比較的容易にできます。さきほどの合同方程式
\[x^2\equiv18\quad (\mathrm{mod}\:31)\]
を満たす最小の整数 $x$ を求めてみます。



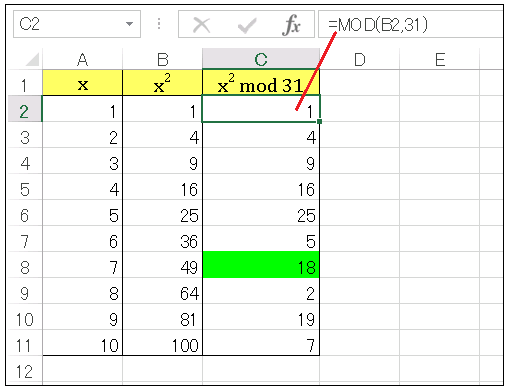
A 列に $1$ から $10$ までの整数、B 列にその平方数、C 列には平方数を $31$ で割った値が並んでいます。余りが $18$ となっているセル（緑色に塗られているところ）があります。すなわち解が $x=7$ であることがわかります。このように問題をビジュアル化できるので、Excel は数論にとって相性の良いツールです。

VBAで平方剰余の問題を解いてみます

VBA で平方剰余の問題を解く QR関数をつくっておきました。QR は Quadratic Residue（平方剰余）の頭文字です。VBE を起動して標準モジュールに貼りつけると、ワークシートで Excel 関数のように扱えます。

'VBA Quadratic Residue

Function QR(a As Long, p As Long) As Variant
　　Dim x As Long

　　'pについてaと合同な最小数を得る
　　Do While a > p
　　　　a = a - p
　　Loop

　　'解が見つからない場合はFalseを返す
　　QR = False

　　'x^2をpで割った余りがaであればxは解
　　For x = 1 To p - 1
　　　　If x ^ 2 Mod p = a Then
　　　　　　QR = x
　　　　　　Exit For
　　　　End If
　　Next x

End Function

QR関数を使うときはセルに「=QR(a,p)」の形で入力します。もし解がなければ（平方非剰余であるならば）、この関数は False を返します。さきほどの合同方程式
\[x^2\equiv18\quad (\mathrm{mod}\:31)\]をこの関数で解いてみましょう。
「=QR(18,31)」と入力すると、7 という値が返ってきます。つまり、$18$ は $31$ の平方剰余であり、方程式の解は $x=7$ です。