真分数列・左右対称群

確率演習【SQ24】～【SQ26】は群数列の問題を集めてみました。【SQ24】はセンター試験を一部変更して掲載しました。マークシート形式を記述式にしてあるので、そこそこ手応えのある問題になっています。特別な発想が求められるわけではありませんが、丁寧に論理を積み上げる必要があります。【SQ25】は一風変わった、真分数の数列です。真分数なんて言葉、小学生の時以来あまり耳にすることもないので、忘れてしまったかもしれませんが、分子が分母より小さい分数のことです。かなり難問かと思います。数列の基礎をしっかり固めてから挑戦してみてください。【SQ26】は左右対称群です。勘の鋭い人は群を見ただけでぴんとくるかもしれません。ひらめけば、短い行数で解答できます。

【SQ24】6 番目の区画に入る項の総和

初項 $-100$、公差 $5$ の等差数列を次のように $1$ 個、$2$ 個、$2^2$ 個、$2^3$ 個 … の区画に分けます。
\[a_1\mid a_2,\ a_3\mid a_4,\ a_5,\ a_6,\ a_7\mid a_8,\ a_9,\ \cdots\]
(1) $M$ 番目の区画の最初の項を $b_M$ とおきます。$b_8$ を求めてください。
(2) $S_8=b_1+b_2+\:\cdots\:+b_8$ を求めてください。
(3) $6$ 番目の区画に入る項の和を求めてください。（センター試験一部改）

【ヒント】各区画に入る項数は等比数列で表されます。
　
【解答】(1) 与えられた数列を $\{a_n\}$ で表すと、一般項は
\[a_n=-100+5(n-1)=5(n-21)\]
で表されます。各区画に入る項数は
\[1,\:2,\:2^2,\:2^3,\:\cdots,\:2^M,\:\cdots\]
のように公比 $2$ の等比級数にしたがって増えていくので、第 $1$ 区画から第 $M$ 区画に入る項数は
\[1+2+2^2+2^3+\:\cdots\:+2^M=\frac{2^M-1}{2-1}=2^M-1\]
となります。したがって、各区画の最初の項 $b_M$ は一般項の $n$ に $2^M-1$ を代入して
\[b_M=5(2^{M-1}-21)\]
で表されることになります。$b_8$ を計算すると
\[b_8=5(2^7-21)=535\]
となります。

(2) $b_M=5(2^{M-1}-21)$ より、
\[S_8=\sum_{M=1}^{8}b_M=5\left(\sum_{M=1}^{8}2^{M-1}-\sum_{M=1}^{8}21\right)=5\left(\frac{2^8-1}{2-1}-21\times 8\right)=435\]
(3) $b_M=5(2^{M-1}-21)$ より、第 $6$ 区画に入る最初の項は
\[b_6=5(2^6-21)=55\]
$n=2^{M-1}$ の関係があったので、$M=6$ のときは $n=2^5$。
すなわち、$b_6$ を数列の一般項で表すと
\[b_6=a_{32}\]
となります。$M=7$ のときは $n=2^6=64$ なので、第 $6$ 区画には
\[a_{32},\:a_{33},\:a_{34},\:\cdots,\:a_{63}\]
のように項が並んでいます。$a_n$ は等差数列なので、$a_{63}$ は第 $7$ 区画の最初の項 $b_7$ から $5$ を引いた数字です。
\[a_{63}=b_7-5=5(2^{7-1}-21)=210\]
したがって第 $6$ 区画は
\[55,\:60,\:65,\:\cdots,\:210\]
というように数字が並びます。項数は $63-32+1=32$ なので、総和を計算すると
\[\frac{32(55+210)}{2}=4240\]
となります。

【SQ25】真分数を並べた数列

真分数を分母の小さい順に、分母が同じ場合には分子の小さい順に並べた数列を $\{a_n\}$ とします。
\[\frac{1}{2},\:\frac{1}{3},\:\frac{2}{3},\:\frac{1}{4},\:\frac{2}{4},\:\frac{3}{4},\:\frac{1}{5},\:\frac{2}{5},\:\frac{3}{5},\:\frac{4}{5},\:\frac{1}{6},\:\cdots\]
真分数 とは分子と分母がともに自然数で、分子が分母より小さい分数 のことです。$k$ を $2$ 以上の自然数とするとき、$\cfrac{1}{k}$ が初めて現れる項を第 $m_k$ 項、$\cfrac{k-1}{k}$ が初めて現れる項を第 $n_k$ 項とします。

(1) $m_k$ を $k$ で表してください。
(2) $n_k$ を $k$ で表してください。
(3) $a_{104}$ を求めてください。
(4) $\{a_n\}$ の初項から第 $n_k$ 項までの和を求めてください。
(5) $\displaystyle\sum_{n=1}^{103}a_n$ を求めてください。

【ヒント】$m_k$ は $k-1$ 群の最初の項、$n_k$ は $k-1$ 群の最後の項です。
　
【解答】数列を群に分けてみます（次のように縦書きすると見やすいです）。

 第 $1$ 群$\quad\cfrac{1}{2}$
 第 $2$ 群$\quad\cfrac{1}{3},\;\cfrac{2}{3}$
 第 $3$ 群$\quad\cfrac{1}{4},\;\cfrac{2}{4},\;\cfrac{3}{4}$
 第 $4$ 群$\quad\cfrac{1}{5},\;\cfrac{2}{5},\;\cfrac{3}{5},\;\cfrac{3}{5}$

分母が $2$ ならば第 $1$ 群、分母が $3$ ならば第 $2$ 群 …… というように、分母と群の番号がひとつだけずれていることに注意しておきます。すなわち分母が $k$ の分数は第 $k-1$ 群に所属しています。

(1) 第 $m_k$ 項は第 $k-1$ 群の最初の項です。$k\geq 3$ のとき、第 $k-2$ 群までに含まれる項数に $1$ を加えれば、$m_k$ が得られることになります。各群の項数はひとつずつ増えていくので、
\[m_k=(1+2+\:\cdots\:+k-2)+1=\frac{(k-2)(k-1)}{2}+1=\frac{k^2-3k+4}{2}\]
この式は $k=2$ のときも成立します。

(2) $\cfrac{k-1}{k}$ は第 $k-1$ 群の末項なので、
\[n_k=1+2+3+\:\cdots\:+k-1=\frac{(k-1)k}{2}\]
となります。

(3) $a_{104}$ が第 $k-1$ 群に属しているとすると、
\[m_k\leq 104\leq n_k\]
が成り立ちます。左辺から $1$ だけ引いておいて
\[m_k-1\lt 104\leq n_k\]
(1) と (2) の結果を代入して
\[(k-2)(k-1)\lt 208 \leq (k-1)k\]
$14^2=196$ なので、$k=15$ を予測して入れてみると、上の不等式を満たすことがわかります。このとき
\[m_k=\frac{(k-2)(k-1)}{2}+1=92\]
なので、$104-92+1=13$ より、$a_{104}$ は第 $14$ 群の第 $13$ 項であることがわかります。よって、
\[a_{104}=\frac{13}{15}\]
となります。

(4) $k\geq 2$ のとき、第 $k-1$ 群に含まれる項の数は
\[\begin{align*}&\frac{1}{k}+\frac{2}{k}+\:\cdots\:+\frac{k-1}{k}\\[6pt]&=\frac{1}{k}\{1+2+\:\cdots\:+k-1\}\\[6pt]&=\frac{1}{k}\frac{(k-1)k}{2}=\frac{k-1}{2}\end{align*}\]
第 $1$ 群から第 $k-1$ 群に含まれる数の和は
\[\sum_{p=2}^{k}\frac{p-1}{2}=\frac{1+2+\:\cdots\:+k-1}{2}=\frac{(k-1)k}{4}\]
となります。

(5) (3) の結果から、$a_{103}$ は第 $14$ 群の第 $12$ 項です。(4) の結果を用いて、第 $1$ 群から第 $14$ 群までに含まれる数、すなわち数列の初項から $a_{105}$ までの総和を計算すると
\[\sum_{n=1}^{105}a_n=\frac{14\cdot 15}{4}=\frac{105}{2}\]
が得られます。ここから $a_{104}$ と $a_{105}$ を引けば、求める答えが得られます。
\[\sum_{n=1}^{103}a_n=\sum_{n=1}^{105}a_n-\frac{13}{15}-\frac{14}{15}=\frac{507}{10}\]

【SQ26】各群の数字が左右対称に並んでいます

ある規則によって並べられた数列 $\{a_n\}$ を $1$ 個, $2$ 個, $3$ 個, … の群に分けます。
\[1\mid 1,\ 1\mid 1,\ 2,\ 1\mid 1,\ 3,\ 3,\ 1\mid 1,\ 4,\ 6,\ 4,\ 1\mid \cdots\]　$a_{158}$ を求めてください。

【ヒント】久しぶりのオリジナル問題です。まだ確率分野の「組み合せ」について学んでいない人は、この問題をパスしてください。「〇〇の三角形」は左右対称に並んでいます。
　
【解答】与えられた数列は、$(a+b)^n$ の展開係数 ($2$ 項係数) を並べたものです。すなわち、パスカルの三角形の各段を上から順に第 $1$ 群、第 $2$ 群 … としたものです。



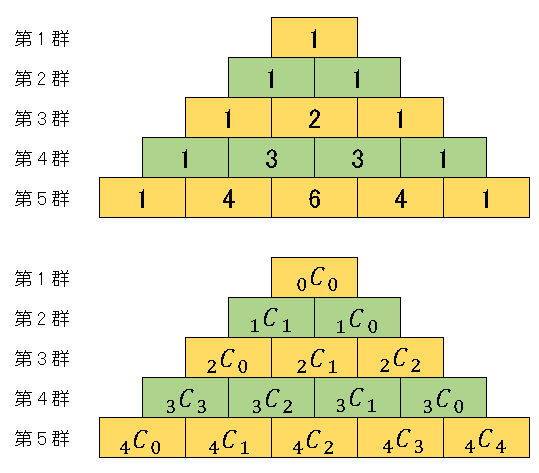
したがって、第 $M$ 群の $k$ 番目の数は
\[{}_{M-1}\mathrm{C}_{k-1}\]
で表されることになります。各群の項数は $1$ 個, $2$ 個, $3$ 個, …… と増えていくので、第 $1$ 群から第 $M$ 群に含まれる項数は
\[f(M)=\frac{M(M+1)}{2}\]
で表されます。$f(17)=153,\ f(18)=181$ なので、$a_{158}$ は第 $18$ 群にあります。また、第 $18$ 群の最初の項から数えると $158-153 = 5$ 項目となります。よって求める答えは
\[a_{158}={}_{M-1}\mathrm{C}_{5-1}={}_{17}\mathrm{C}_{4}=\frac{17!}{4!(17-4)!}=2380\]
となります。