今回の講座では三角形の面積を求めるヘロンの公式を VBA で実装してみます。一見すると簡単に実装できそうに思えますが、とりうる引数について制限があるので、完璧な実装には色々と考えなければならない点も多く、プログラミング入門用としてなかなか良い題材です。単純な実装から始めて、少しずつ問題点を改善しながらマクロを完成させていきます。
【VBA】ヘロンの公式で三角形の面積を計算する
三辺の長さが与えられている場合、三角形の面積はヘロンの公式
\[S=\sqrt{s(s-a)(s-b)(s-c)}\]
によって計算できます。ここに $2s=a+b+c$ です。たとえば、一辺の長さが $1$ の正三角形の場合、
\[s=\frac{a+b+c}{2}=\frac{1+1+1}{2}=\frac{3}{2}\]
なので、面積は
\[S=\sqrt{\frac{3}{2}\left(\frac{3}{2}-1\right)^3}=\frac{\sqrt{3}}{4}=0.433\]
と計算できます。ヘロンの公式の証明は記事の後半に載せてあるので、気になる人は確認しておいてください。それではさっそく、ヘロンの公式を VBA で実装してみましょう。
'[VBA] ヘロンの公式(1) Function HERON_1(a As Double, b As Double, c As Double) As Double Dim s As Double, t As Double s = (a + b + c) / 2 HERON_1 = Sqr(s * (s - a) * (s - b) * (s - c)) End Function
Sqr は渡された数値の平方根をとる関数です。辺の長さが $1$ の正三角形の面積を HERON_1 関数で計算させてみましょう。ワークシートのセルに
=HERON_1(1,1,1)
と入力すると 0.433 の値が返ります。これで特に問題なさそうですが、実はこのままでは不十分です。たとえば、
=HERON_1(1,1,2)
と入力すると 0 を返してしまいます。何かコードにミスがあったのでしょうか? 手計算で確かめてみましょう。$s$ を計算すると、
\[s=\frac{a+b+c}{2}=\frac{1+1+2}{2}=2\]
となるので、これをヘロンの公式に代入してみると…
\[\begin{align*}S=&\sqrt{s(s-a)(s-b)(s-c)}\\[6pt]=&\sqrt{2(2-1)(2-1)(2-2)}\\[6pt]=&0\end{align*}\]
$(s-c)$ の部分が $0$ になるので、やはり結果は $0$ で間違いなさそうです。こんな計算をしなくても、勘の良い人であれば、「底辺の長さが $2$ で、残る二辺の長さが $1$ の二等辺三角形など存在するはずがない」ことに気づいたかもしれません(敢えて極限として考えるなら、完全に潰れた三角形の面積は $0$ といえます)。
よく知られているように、三角形の各辺の長さは自由にとれるわけではなく、「二辺の長さを加えた値は他の一辺の長さより大きい」という条件で束縛されています。
$a=b=1,\ c=3$ のような値を入れてみると、ヘロンの公式では √ の中身が負になって、面積が虚数となってしまいます。さきほど実装した HERON 関数で、
=HERON(1,1,3)
と入力すると、#VALUE! エラーが発生します。VBA の Sqr 関数に負の値が渡されたことに起因します。
このように、ヘロンの公式に「三角形として成立しない辺の組」を入れると $0$ や虚数を返します。ある意味、数値計算にとって、これはとても便利な公式といえます。三辺について「二辺の長さを加えた値は他の一辺の長さより大きい」という条件をコードに落とし込むよりも、ずっと簡単でわかりやすいからです。つまり、ヘロンの公式の √ の中身
\[t=s(s-a)(s-b)(s-c)\]
が 0 や負の場合に、エラーを返すように実装すればよいことになります。$t$ が負の場合はどのみち #VALUE! を返すので、特に処理する必要はないと思うかもしれません。しかし、#VALUE! は「入力した数式または参照先のセルに問題があります」という警告です。今の場合は Sqr 関数に負値が渡されたからだとわかっていますが、一般には #VALUE! の発生理由は多肢にわたり、原因の特定は面倒です。そこで、「関数に無効な数値が含まれている」ことを警告する #NUM! エラーを発生させたほうが、ユーザーにはわかりやすいでしょう。また、$t$ が $0$ になる場合も負値となる場合も、同じエラーを送出するようにしたほうが、より親切な設計だといえます。
VBA では CVErr() にエラー番号またはエラー定数を渡して、特定のエラーを発生させられます。ここではエラーについては深入りしません。とりあえず、次の関数をワークシートで実行して、CVErr(XlErrNum) が #NUM! エラーを返すことだけ確認してください。
'[VBA] エラーテスト関数 Function error_test() error_test = CVErr(xlErrNum) End Function
さきほどのコードを改良してみましょう。
'[VBA] ヘロンの公式(2) Function HERON_2(a As Double, b As Double, c As Double) As Variant Dim s As Double, t As Double s = (a + b + c) / 2 t = s * (s - a) * (s - b) * (s - c) If t <= 0 Then HERON_2 = CVErr(xlErrNum) Else HERON_2 = Sqr(t) End If End Function
HERON_2 関数の戻り値のデータ型は Variant型で宣言しています。Variant はどのような型のデータでも格納できる便利なデータ型です。戻り値が数値でなくエラーメッセージとなる可能性があるので、この型を選んでいます。
入門講座では初めてとなる、条件分枝を記述する If ステートメントが登場しています。If ステートメントは
If [条件] Then [条件]を満たした場合の処理 Else [条件]を満たさなかった場合の処理 End
のような形で記述します。上のコードの
If t <= 0 Then HERON = CVErr(xlErrNum) Else HERON = Sqr(t) End If
の部分では、t が 0 以下なら #NUM! を返し、それ以外の場合は t の平方根をとって面積を返すようにしています。ワークシートの適当なセルに
=HERON_2(1,1,2)
と入力して、0 ではなく #NUM! を返すことを確認してください。
これで完成 … と思いきや、まだ問題があります。
=HERON_2(-1,-1,-1)
と入力すると、0.433 が返ります。実はヘロンの公式は、辺の長さが負であっても計算結果が正の実数になることがあります。数学の問題を解く時に、わざわざ負の長さを代入することはまずないので、公式に $a,\ b,\ c$ が正であると明示されていないこともありますが、プログラミングにおいては、このようなイレギュラーな事態にも備えておく必要があります。このことも踏まえて、ヘロンの公式の完成版は次のようなコードになります。
'[VBA] ヘロンの公式(3) Function HERON(a As Double, b As Double, c As Double) As Variant Dim s As Double, t As Double s = (a + b + c) / 2 t = s * (s - a) * (s - b) * (s - c) If t <= 0 Or a <= 0 Or b <= 0 Or c <= 0 Then HERON = CVErr(xlErrNum) Else HERON = Sqr(t) End If End Function
今度は
=HERON(-1,-1,-1)
と入力すると、#NUM! エラーを返すことを確認してください。
ヘロンの公式の証明
ヘロンの公式を証明しておきます。下図のような三角形を考えます。
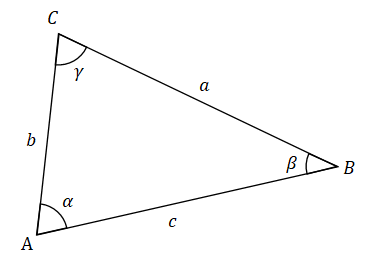
頂点 $A$ から辺 $BC$ に垂線を下ろし、$BC$ と交わる点を $H$ とします。
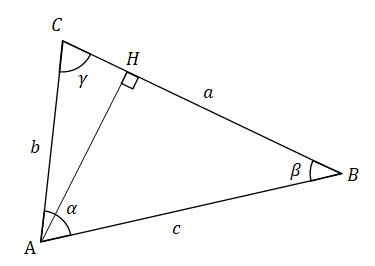
$AH$ の長さは $b\sin{\gamma}$ なので、三角形 $ABC$ の面積は
\[S=\frac{ab}{2}\sin{\gamma}\tag{1}\]
と表せます。三角関数の公式 $\sin^2{\gamma}=1-\cos^2\gamma$ を使うと、
\[\begin{align*}S&=\frac{ab}{2}\sqrt{1-\cos^2{\gamma}}\\[6pt]&=\frac{ab}{2}\sqrt{(1+\cos{\gamma})(1-\cos{\gamma})}\tag{2}\end{align*}\]
となります。さらに余弦定理 $c^2=a^2+b^2-2ab\cos{\gamma}$ により、
\[\cos{\gamma}=\frac{a^2+b^2-c^2}{2ab}\tag{3}\]
と表せるので、これを式 (2) に代入して整理すると、
\[S=\frac{1}{4}\sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)}\tag{4}\]
を得ます。ここで、
\[a+b+c=2s\tag{5}\]
とおくと、
\[\begin{align*}b+c&=2s-a\\[6pt]c+a&=2s-b\\[6pt]a+b&=2s-c\end{align*}\tag{6}\]
と表せるので、これを (4) に入れて式を整理すれば、
\[S=\sqrt{s(s-a)(s-b)(s-c)}\tag{7}\]
となって、ヘロンの公式が得られました。■

エクセルや数学に関するコメントをお寄せください