【Excel】数値積分
今回の Excel 数学講座はエクセルで積分してみようという内容です。積分と聞くとなんだか難しそうな気がするかもしれませんが、実のところコンピュータは微分よりも積分のほうが得意なので、意外と簡単な作業です。エクセルの操作に慣れている人なら 15 分ほどで終わってしまうと思います。この記事で作成するワークシートをダウンロードすることもできるので、ゼロからシートを作成するのが難しそうだと思う人はダウンロードして、中身を確認しながら本記事を読んでみてください。
≫ 数値積分のワークブック (excel_integ.xlsx) をダウンロード
台形公式を用いた数値積分
数値積分には色々な方法がありますが、今回は比較的簡単な「台形近似」という方法を使って定積分を求めます。台形近似公式の詳しい導き方を知りたい人は台形公式による数値積分という記事に載っているので、そちらを参照してください。ここでは概念図と公式だけ載せておきます。
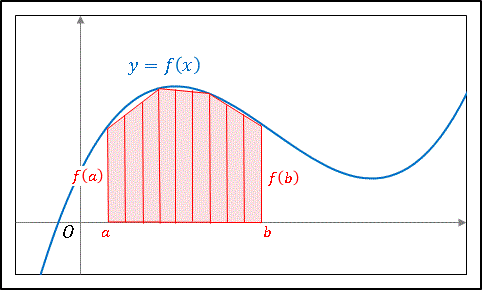
区間 [a, b] において、ある関数 y=f(x) と x 軸に囲まれた面積は
\[\int_{a}^{b}f(x)dx\simeq \left\{ \frac{f(a)+f(b)}{2}+\sum_{k=1}^{n-1}f\left( a+k\Delta x \right) \right\} \Delta x\]
という式で近似されます。ここで
\[\Delta x=\frac{b-a}{n}\]
は切り分けたうちの 1 区分の長さです。
【Excel】三次関数の数値積分
それでは実際にエクセルで定積分を計算してみましょう。三次関数
\[f(x)=x^3+x^2+x+1\]
を 0 から 1 まで積分してみます。区間は 10 等分することにします。つまり ⊿x = 0.1 です。次のようなワークシートを作ります。
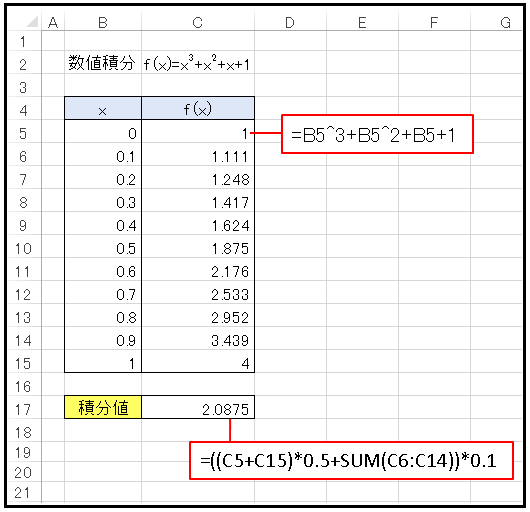
セル C5 には
=B5^3+B5^2+B5+1
と入力してセルの右下隅をダブルクリックしてセル C15 まで値を埋めます。これが各点における関数の値です。そしてセル C17 には台形面積の和（積分の近似値）を入力します。
=((C5+C15)*0.5+SUM(C6:C14))*0.1
端点である f(0) と f(1) にはそれぞれ 1/2 = 0.5 を掛けて足し合わせ、それ以外の f(x) はそのまま足します。最後に式全体に区分の長さ ⊿x = 0.1 を掛けて面積を計算しています。その結果は 2.0875 となっていますね。ちなみに実際の値は 2.0833 ですから、かなり良い精度の近似であることがわかります。もちろん ⊿x をもっと小さな値にすれば、さらに精度が向上します。
【Excel】log(x)sin2xの数値積分
手計算では扱いにくいような複雑な積分であっても、数値計算では比較的簡単に求めることができます。例として、$f(x)=\log x\sin^2 x$ を $0$ から $\pi$ まで積分してみます。
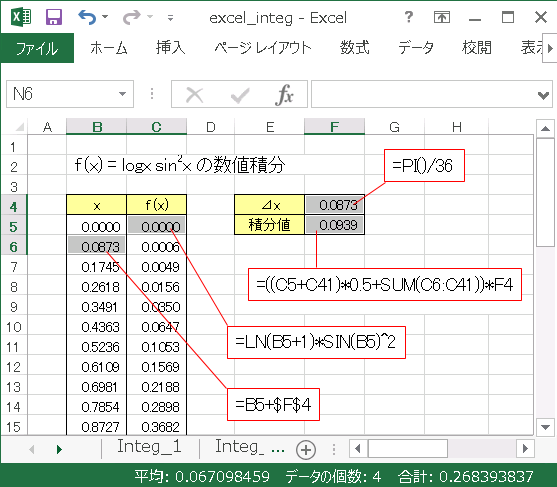
上図にあるように、セル F4 に $\pi$ を $36$ 等分した値を入れておきます：
=PI()/36
これが $\delta x$ です。セル B5 に 0 を入れ、セル B6 には
=B5+$F$4
と入力して、数式をセル B41 までコピーします。これで $0$ から $\pi$ までの値が埋まります。セル C2 には
=LN(B5+1)*SIN(B5)^2
と入力し、数式をセル C41 までコピーします。最後にセル F2 に台形公式
=((C5+C41)*0.5+SUM(C6:C41))*F4
を入力して積分値 $0.0939$ を得ます。
【Amazon書籍紹介】Excelで学ぶ微分積分
Excel を使って初歩から微分積分を学ぶなら、『Excelで学ぶ微分積分』(ナツメ社) がおすすめです。
Excelで学ぶ微分・積分?Excelで微分・積分を学習すれば、いろいろと実感を伴って理解できる 中古価格 |  |
かなり古い本 (2003年初版発行) ですが、説明がわかりやすくて本当に良書です。個人的には 100 点満点中 90 点の評価をつけたいぐらいです。本書は、微分積分の基礎概念と数値的に扱う方法を同時に学べるようになっています。Excel のグラフ機能を活用することで、直感的・視覚的に微分積分のイメージを定着させることができます。普通の学び方では、関数の極限を頭の中でイメージするのはなかなか難しいのですが、Excel を使えば、関数がどのように一定の値に収束していくかを実際に目で確認することができます。数学を専攻する人以外の、数学を道具として活用したい理工系の学生や研究者にとっては、厳密性よりもイメージの定着を図って数学を学ぶほうが大切だと思うので (あくまで個人的見解です)、そういう意味でも、本書のような数値計算の入門書は重宝します。
第１章で Excel の基本操作 (主にグラフウィザードを使ってデータを可視化する手順) を習得した後で、第２章で微分、第３章で積分を学ぶ構成になっています。第４章では微分方程式、フーリエ級数、ラプラス変換、確率微分など、微分積分のやや高度な応用について解説しています。第４章の二階線形微分方程式のあたりまで読めば、微分積分の基礎知識を一通り身につけられます。残りは必要に応じて選択すればよいでしょう。
古い本なので、さすがに付属品の CD-ROM の動作は保証できませんが、ワークシートは全て手入力しないと身につかないので、CD-ROM は特に必要ないと思います。私自身も一度も使ったことがありません。シートをゼロからコツコツつくるのも案外楽しい作業なので、焦らずにスローステップ学んでみてください。
エクセルや数学に関するコメントをお寄せください
【AI連載小説】数学のリズム、エクセルの旋律(8)
「Excelを活用して積分を教えます」
ある日の夕方、研伸はアルバイトの家庭教師として、石川由紀の家に向かっていました。由紀は高校生で数学に苦手意識を持っており、積分の理解に課題を感じていました。研伸はExcelを使って、積分の基本的な概念を分かりやすく説明しようと考えていました。
研伸：こんにちは、由紀さん。今日は積分の勉強を進めていきましょうか？
由紀：こんにちは、研伸さん。積分って難しいんですよね。
研伸：大丈夫です。実際の応用例を見ながら、Excelを使って積分を考えてみましょう。まず、f(x)=x^2 の関数を考えてみますね。
（研伸は由紀にExcelを開かせ、x の範囲や積分の幅を変えながら、関数の面積を求めるデモンストレーションを行います）
研伸：これで、数値積分の考え方を理解できましたか？
由紀：なるほど、Excelを使えば関数の面積を簡単に求められるんですね。でも、具体的にどうやるんですか？
研伸：いいえ、これから具体的な計算手順を見ていきます。まず、ExcelのA列に x の値を、B列に f(x) の値を入力します。
（研伸は由紀にExcelのシートに数値を入力する手順を教えながら、関数の近似的な積分を行います）
研伸：そして、SUMPRODUCT関数を使って f(x) と幅（Δx) をかけ合わせ、その総和を取ります。これが数値積分の近似値です。
由紀：（Excelを見ながら）なるほど、こうやって計算するんですね。でも、これってどれくらいの精度があるんですか？
研伸：精度は Δx を小さくすることで向上します。ただし、細かくしすぎると計算が複雑になるので、バランスが大切です。
由紀：（納得して）なるほど、バランスですね。Excelを使えば積分の近似値が簡単に求められるんですね。ありがとうございます、研伸さん。
（由紀は徐々に積分の理解が進んでいくのを感じ、研伸も生徒の理解度に合わせながら、数学の楽しさを伝えていきました）
Excelで積分したいのですがy=sqrt(x)のグラフ、0からxまでの積分2/3xsqrt(x)＋Cおよび積分の近似のグラフの求め方を知りたいです。範囲は0から3で0.1刻み。積分定数C=0でお願いします
次のファイルダウンロードしてください。
➡ファイルをダウンロード
f(x)=sqrt(x) と F(x) = (2x/3)sqrt(x) のグラフがプロットしてあります。
ファイルの内容について疑問点がありましたら、またコメント欄でご質問ください。