Excelで微分する

この記事では、関数の微分についての初歩からの説明と、Excel を用いた数値微分の方法について解説します。

微分係数と導関数

$y=f(x)$ はある区間で連続であるとします。その区間内で $x$ の値が $a$ から $a+h$ に変化すると $y$ の値は $f(a)$ から $f(a+h)$ へと変化します。



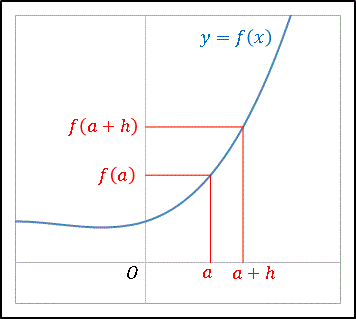
このとき極限
\[f'(a)=\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}\]
が存在するならば、 $f(x)$ は $x=a$ で微分可能であるといい、この有限確定値 $f'(a)$ を $x=a$ における 微分係数 (differential coefficient) とよびます。また $f'(a)$ は $x=a$ に引いた接線の傾きを表しています。例として $f(x)=x^2$ の $x=a$ における微分係数を求めてみます。
\[f'(a)=\lim_{h\rightarrow 0}\frac{(a+h)^2-a^2}{h}=\lim_{h\rightarrow 0}(2a+h)=2a\]
$a$ は任意の値ですから、 $f(x)=x^2$ は実数全域で有限確定値 $2a$ をもちます。
すなわち $f(x)=x^2$ は実数全域で微分可能だということです。

$h$ が正の方向（ $x$ 軸の右側）から近づくときの極限
\[f'(a+0)=\lim_{h\rightarrow +0}\frac{f(a+h)-f(a)}{h}\]
のことを右方微分係数、$h$ が負の方向（ $x$ 軸の左側）から近づくときの極限
\[f'(a-0)=\lim_{h\rightarrow -0}\frac{f(a+h)-f(a)}{h}\]
のことを左方微分係数といいます。右方微分係数と左方微分係数は限定された区間で定義されるような関数の端点での微分係数を求めるときに用います。たとえば $x \geq a$ で定義された $f(x)$ について、$x=a$ で右方微分係数が存在するならば $f(x)$ は微分可能であるといいます。

ある区間の各点 $x$ において $f(x)$ が微分可能であるとき、すなわち上で述べたような極限値（微分係数）をもつとき、$f(x)$ はその区間において微分可能であるといいます。このときの微分係数 $f'(x)$ はその区間で定義された $x$ の関数です。$f'(x)$ のことを $f(x)$ の 導関数 (derived function) とよび、$f'(x)$ を求めることを $f(x)$ を微分するといいます。



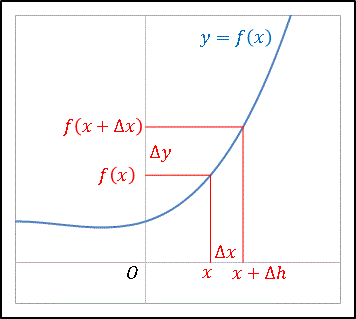
区間内で $x$ から $x+\Delta x$ に変化するとき、$y$ の変化を $\Delta y$ で表すと、$y=f(x)$ の導関数 $f'(x)$ は
\[f'(x)=\lim_{\Delta x \rightarrow +0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x \rightarrow +0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\]
と表されます。幾何学的には導関数 $f'(x)$ は曲線 $f(x)$ 上の任意の点における接線の傾きを表しています。 $y=f(x)$ の導関数を表す記号は他にも
\[y’,\quad \frac{dy}{dx},\quad \frac{df(x)}{dx}\]
などがあります。例として $f(x)=x^3$ の導関数を求めてみます。
\[f'(x)=\lim_{\Delta x \rightarrow +0}\frac{(x+h)^3-x^3}{\Delta x}=\lim_{\Delta x \rightarrow +0}(3x^2+3x\Delta x)=3x^2\]

Excelによる数値微分

Excel で微分係数を計算してみましょう。紙の上で微分するときは、三角関数なら三角関数の、指数関数なら指数関数の微分公式を使って計算しますね。しかしコンピュータ上で微分を再現するときには、$x = a$ における微分係数を表す
\[f'(a)=\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}\]
という式を使うと上手く計算できます。ただ、コンピュータでは厳密な極限をとることはできないので、「とても小さな h 」をとることで我慢して近似計算を行うことになります。今回は対数関数
\[f(x) = \log x\]
について、その導関数 $f'(x)$ と並べて表示させてみます。さっそくシートの概観を見てみましょう。



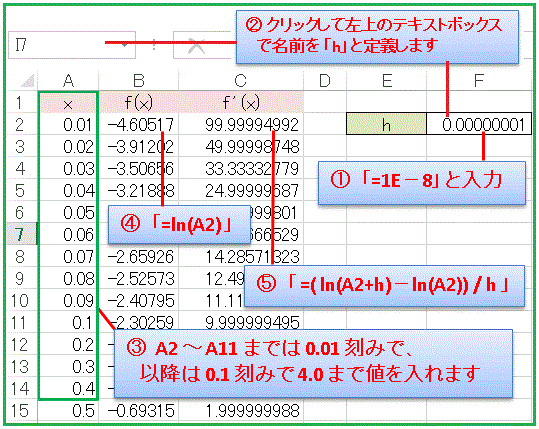
この図だけで「もうわかったよ」という人は、さっそく自分のエクセルを立ち上げて試してみてください。「まだちょっとわからないところがある」という人は以下の説明に目を通してください。

セル F2 には h つまり「とても小さな数」を入れます。どのくらいが「とても小さな数」なのかは難しいですが、とりあえず「 1 億分の 1 」ぐらいにしておきます。そこでセル F2 に

=1E-8

と入力しておきましょう。これは $10^{-8}$ という数を表しています。

普段は A5 や G10 などのようにアルファベットと数字でセル番地を指定していますが、実はこの番地に名前をつけることもできます。 F2 を選択した状態で左上のテキストボックスに「h」と書きこんで Enter を押して名前を定義しておきます。こうすることで、今後は「h」という文字でこのセルを参照することができるようになります。

対数関数ですから、真数条件 $x\lt 0$ に注意します。 0.01 から 0.1 までは 0.01 刻みで、それ以降は 0.1 刻みで入力しておきます。底を $e$ とする対数関数は Excel では ln() です。B2 に

=ln(A2)

と入れて右下隅のフィルハンドルをダブルクリックして列にデータを埋めます。また C2 には微分係数を表す

=(ln(A2+h)-ln(A2))/h

という式を入力して列にデータを埋めます。

B 列と C 列を選択して [挿入タブ] から [散布図] 、 [平滑線] の順に選択します。縦軸の範囲を －4 ～ 4, 横軸の範囲を 0 ～ 4 あたりに設定してグラフを描くと次のようになります。



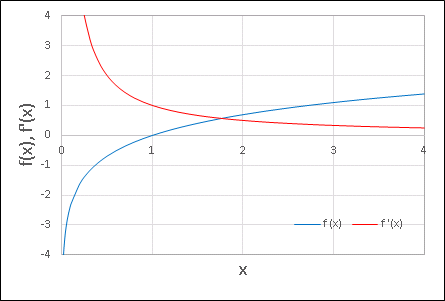
$y = f'(x)$ のグラフは $y = 1 / x$ と非常によく一致します。

ワークシートへの入力作業が面倒な人は、以上の内容がすべて記載された Excel ファイルをダウンロードできるので、是非お試しください（≫ ファイルをダウンロード）。

より精度の高い数値微分の１つに 中心差分公式 とよばれる手法があります。連続関数 $f(x)$ を、$a$ の近くでテイラー展開すると、
\[\begin{align*}f(a+h)=f(a)+f'(a)h+\frac{f^{\prime\prime}(a)h^2}{2!}+\frac{f^{\prime\prime}(a)h^3}{3!}+\cdots\\[6pt]f(a-h)=f(a)-f'(a)h+\frac{f^{\prime\prime}(a)h^2}{2!}-\frac{f^{\prime\prime}(a)h^3}{3!}+\cdots\end{align*}\]
となるので、$h$ の 2 次以上の項を無視すると
\[f'(a)=\frac{f(a+h)-f(a-h)}{2h}\]
が得られます。これが中心差分公式です。

$f(x)=\sin x$ について、中心差分公式によって得られた微分係数を理論値と比較してみます。以下のようなワークシートを用意します。

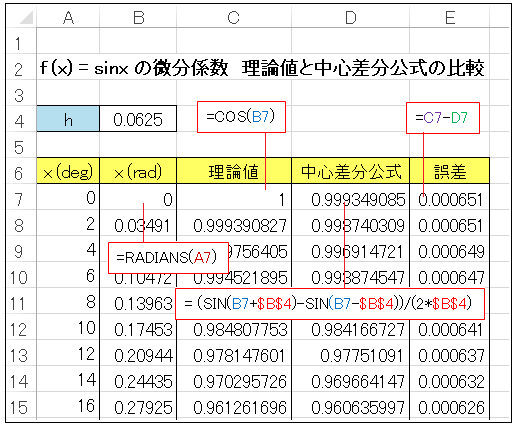
セル B4 には $h$ の値として 1/16 = 0.0625 を用意してあります。A 列には度数単位で角度を入れ、B 列には A 列の値を RADIANS 関数でラジアン単位に変換した値を入れます。C 列には理論値を入れます。$\sin x$ の導関数は $\cos x$ なので、セル C7 には

=COS(B7)

と入力して数式を下までコピーします。D 列には中心差分公式による微分係数の値を入れます。セル D7 には

=(SIN(B7+$B$4)-SIN(B7-$B$4))/(2*$B$4)

と入力して下までコピーしておきます。E 列には理論値と差分公式による値の差を入れるので、セル E7 には

=C7-D7

と入力します。$h=1/16$ では有効数字 2 桁程度しか一致しないので、あまり精度が良いとは言えませんが、$h$ の値を小さくすることで精度を高めることができます。たとえば $h=1/256$ とすると、$x=\pi/6$ で

理論値：0.866025404　中心差分公式：0.866023201

が得られます。誤差は 1.76661E-06 です。ただし $h$ を小さくしすぎると、数値計算特有の丸め誤差や桁落ちなどが入り込んでくるので、そのあたりを上手く見極めなくてはなりません。