【Excel】等比数列と等比級数 (幾何級数)

等比数列と等比級数

　隣り合う二項の比が一定数 \(r\) であるような数列 \(a_{n+1}=ra_n\) のことを 等比数列 あるいは 幾何数列 (geometric progression) とよびます。また定数 \(r\) は 公比 (common ratio) とよばれます。等比数列の各項を足し合わせたものを 等比級数 (geometric series) といいます。

　初項 1, 公比 $r$ の等比数列の一般項は

\[a_n=r^{n-1} \tag{1}\]
で表され、$n$ 項までの和（有限等比級数）は $r=1$ のとき

\[S_n=n \tag{2}\]

となり、$r \neq 1$ のとき

\[S_n=\frac{1-r^n}{1-r} \tag{3}\]
となります。無限等比級数は $|r| \lt 1$ のときのみ収束して

\[S=\frac{1}{1-r} \tag{4}\]
という値をもちます。$|r| \geq 1$ のときは発散します。初項が $a$ の場合は各公式に $a$ をかけます。

【(1)の証明】初項 1, 公比 \(r\) の等比数列を具体的に書き並べると
　
\[1,\quad r,\quad r^2,\quad r^3,\quad \cdots\]
のようになります。各項について

　　第 1 項　　\(1 \times r^0\)
　　第 2 項　　\(1 \times r^1\)
　　第 3 項　　\(1 \times r^2\)

のように項番号と \(r\) の肩にある数字が 1 つだけずれているので、一般項は
　
\[a_n=r^{n-1} \tag{1}\]
と書き表せます。
　
【(2)(3)の証明】\(r=1\) のときは
　
\[S_n=1+1+1+\: \cdots \:+1=n\]
となります。 \(r \neq 1\) のときは \(S_n\) と \(rS_n\) を具体的に書き並べると、
　
\[\begin{align*}S_n=1+r+r^2+ \: \cdots \: +r^{n-2}+r^{n-1}\\[6pt]
rS_n=r+r^2+r^3 \: \cdots \: + r^{n-1}+r^n\end{align*}\]
となります。両式の差をとると 2 つの項だけが残って
　
\[(1-r)S_n=1-r^n\]
となるので、
　
\[S=\frac{1-r^n}{1-r} \tag{3}\]
が得られます。
　
【(4) の証明】\(r=1\) のときは先の公式
　
\[S_n=n \tag{2}\]
において \(n \rightarrow \infty\) で発散します。\(|r| \gt 1\) のときは公式
　
\[a_n=r^{n-1} \tag{1}\]
において数列が発散するので級数も発散します。\(|r| \lt 1\) のときは公式
　
\[S=\frac{1-r^n}{1-r} \tag{3}\]
において \(n \rightarrow \infty\) とすると、\(r^n\) の項が 0 となるので
　
\[S=\frac{1}{1-r} \tag{4}\]
が得られます。例として初項 $1$、公比 $1/2$ の等比数列の一般項と和を求めてみます。\(r=1/2\) なので一般項は
　
\[a_n= \left( \frac{1}{2} \right)^{n-1}\]
となります。有限項の和は
　
\[S_n=\frac{1-\left( \cfrac{1}{2} \right)^n}{1-\cfrac{1}{2}}=2-\left( \frac{1}{2} \right)^{n-1}\]
となり、この式で \(n \rightarrow \infty\) の極限をとると無限級数の値 \(S=2\) を得ることができます。
　
　初項 \(a\) の等比数列の一般項
　
\[a_n=ar^{n-1}\]
において両辺の対数をとると
　
\[\log a_n=\log a+(n-1) \log r\]
のように書けるので、数列 \(\log a_n\) は初項 \(\log a\), 公差\(\log r\) の等差数列となります。
　
　等比数列の任意の連続した 3 つの項 \(a,\:b,\:b\) について
　
\[b^2=ac \quad (b \neq 0) \tag{5}\]
が成り立ちます。

【(5) の証明】公比を \(r\) とすると
　
\[\frac{b}{a}=\frac{c}{b}=r\]
が成り立つので、
　
\[b^2=ac \quad (b \neq 0) \tag{5}\]
が得られます。

Excelで等比数列と各項の和を計算します

　Excel では等比数列の二項間の関係
　
\[a_{n+1}=a_n r\]
で数列を作成できます。また、第 $n$ 項までの等比数列の和は、各セルを順次足していくという手法を用いるので、
　
\[S_n=S_{n=1}+a_n\]
という関係式で計算させます。初項 1, 公比 3 の等比数列を計算してみます。下図を参照にシートを作ってください。

　

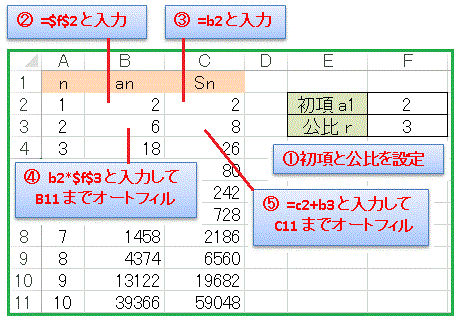
　・F2 に初項 a₁, F3 に公比 r を設定しておきます。

　・n の下には 1 から 10 までの数列番号を用意しておきます。

　・B2 には絶対参照で「=$f$2」と入力して初項が入るようにします。

　・C2 には「=b2」と入力して S₁ = a₁ となるようにします。

　・B3 は「初項×公比」ですから「=b2*$f$3」と入力します。

　・B11 セルまでオートフィルして数列の一般項のデータを完成させます。

　・C3 は S₁ に a₂ を加えた S₂ が入ります。
　
　・「=c2+b3」と入力してオートフィルしておきましょう。

　以上で等比数列の一般項と和のデータが揃いました。

　公比 r を 1/2 = 0.5 に変更してみましょう。

　

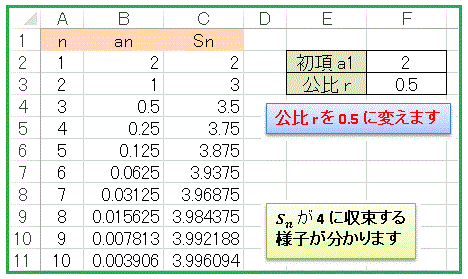
　公比の変更に応じて一般項と総和のデータも更新されますが、注目すべきは S_n の最後のほうのデータです。n の増加に対して数値にほとんど変化がなく、4 に近づいている様子が見えますね。実際、[3] の公式を使って
　
\[S_{n}=\frac{2(1-0.5^{n})}{1-0.5}\]
において $n\rightarrow\infty$ とすれば $S_{n}\rightarrow 4$ という極限値が得られますが、その収束は非常に速く、$n=10$ においてすでに $S \simeq 4$ とみなしてよいことがわかりますね。