この記事では、虚数と複素数についての基本事項と、Excel のエンジニアリング関数による複素数計算について解説します。
【Excel】虚数と複素数
平方 ($2$ 乗) して $-1$ になる数 $i$ を定義し、虚数単位とよびます。
\[i^2 \equiv -1 \tag{1}\]
虚数単位 $i$ と実数のペア $(a,\ b)$ を次のような形で結びつけた数を 複素数 (complex number) と定義します。
\[z \equiv a+bi \tag{2}\]
複素数とは単位 (素) が “$1$” と “$i$” の $2$ 種類(複)あることを示す用語です。実数 $a,\ b$ を、それぞれ実部 (real part)、虚部 (imaginary part) とよび、それぞれ
\[a=\mathrm{Re}(z),\quad b=\mathrm{Im}(z)\tag{3}\]
のように表します。
複素数 $z_1=a+bi,\ z_2=c+di$ について、四則演算 (加減乗除)は次のように定義されています。
\[\begin{align*}z_1 + z_2&=(a + c)+(b + d)i\tag{4}\\[6pt]z_1-z_2&=(a-c)+(b-d)i\tag{5}\\[6pt]z_1 z_2&=ac-bd+(ad+bc)i \tag{6}\\[6pt]\frac{z_1}{z_2}&=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i\tag{7}\end{align*}\]
横軸 $x$ を実部, 縦軸 $y$ を虚部として座標を設定すると、複素数 $z=x+iy$ を平面上の1点に対応させられます。
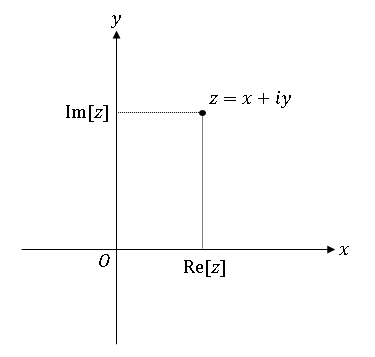
このような平面を複素平面 (complex plane)、またはガウス平面(Gaussian plane)とよびます。
$z=a+bi$ の絶対値 (大きさ) は、複素平面上で原点と $(a, b)$ を結んだ線分の長さになるように定義されています。
\[|z| \equiv \sqrt{a^2+b^2}\tag{8}\]
ある複素数 $z=a+bi$ について虚部の符号を反転させた数を共役複素数 (complex conjugate) とよび、
\[\bar{z}=a-bi\tag{9}\]
と書きます。$z$ と $\bar{z}$ は複素平面上で実軸について対称な点となります。$z$ と $\bar{z}$ の積をつくると
\[z \bar{z}=(a+bi)(a-bi)=a^2+b^2\tag{10}\]
となるので、複素数の絶対値は共役複素数を用いて
\[|z|=\sqrt{z\bar{z}} \tag{11}\]
と表すこともできます。
複素数 $z_1=a+bi,\ z_2=c+di$ について、$z_1 z_2$ の絶対値を計算すると
\[|z_1 z_2|=\sqrt{(a^2+b^2)(c^2+d^2)}=|z_1||z_2| \tag{12}\]
となります (複素数の積の絶対値は各々の絶対値の積に等しくなっています)。
Excel には複素数を演算するためのエンジニアリング関数が一通り揃っています。これらの関数は a+bi あるいは a+bj の形式で記述された文字列を複素数として認識して受け取ります (a, b は任意の数値)。complex_2.xslx の “基本演算” シートには、主な関数の演算例を載せています。必要な方はファイルをダウンロードしてください。
≫ complex_2.xslx をダウンロード
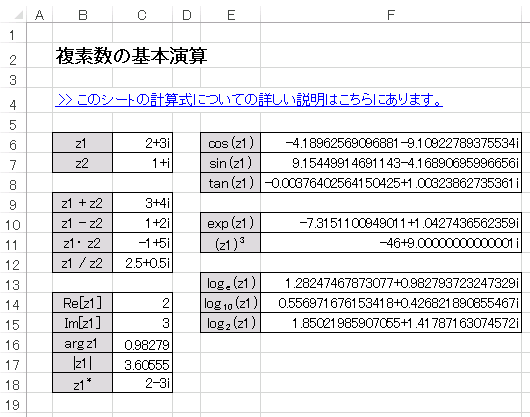
セル C6 には文字列 2+3i、C7 には 1+i が入力されています。
セル C9 には
=IMSUM(C6,C7)
が入力されていて、2+3i と 1+i の加算 3 + 4i が表示されています。同様に、セル C10, C11, C12 には
=IMSUB(C6,C7) =IMPRODUCT(C6,C7) =IMDIV(C6,C7)
が入力され、減算、乗算、除算を実行しています。
複素平面における原点からの距離 $r$ と 偏角 $\theta$ を使って
\[z=re^{i\theta}=r(\cos\theta + i\sin\theta) \tag{12}\]
と表すことを複素数の極形式とよびます (下図参照)。
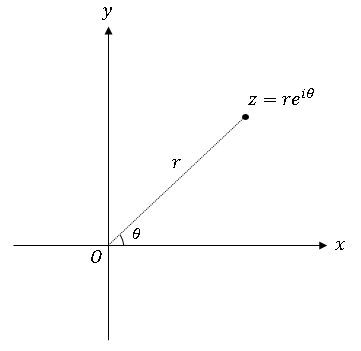
argument (偏角) の略語を使って、$\theta$ を $\mathrm{arg}z$ と書くこともあります。
$z$ の絶対値を定義に従って計算すると
\[|z|=r\sqrt{\cos^2 \theta + \sin^2 \theta}=r\tag{13}\]
となるので、極形式の複素数は
\[z=|z|e^{i\theta}=|z|(\cos\theta + i\sin\theta) \tag{14}\]
と書き直せます。
複素数 $z=a+bi$ を極形式 $z=|z|e^{i\theta}$ に変換するには、$|z|$ の他に偏角 $\theta$ を求める必要があります。原点と複素平面上の点 $a+bi$ を結ぶ線分の傾き
\[\tan\theta=\frac{b}{a}\tag{15}\]
から計算できますが、一般に手計算では困難です。Excel には複素数の偏角を求める IMARGUMENT 関数が用意されています。セル C16 には
=IMARGUMENT(C6)
と入力して、z1 の偏角の値が計算されています。
complex_2 ブックの “極形式” シートでは、偏角 $\theta$ を変化させて、複素平面に円をプロットしています。
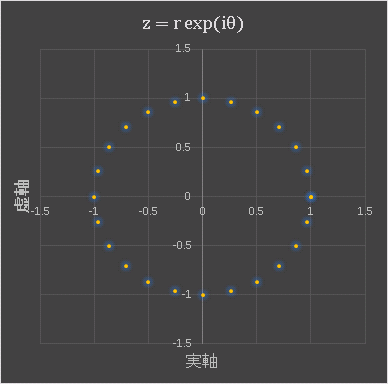
シートの中身に関心がある人は、ダウンロードしたブックを開いて数式を確認してみてください。同じブックの “らせん” シートでは、ちょっとした遊びで、複素平面に螺旋を描いています。そちらもぜひご覧ください。
以下では、Excel の複素数演算に使用する主なエンジニアリング関数を列挙して解説します。
COMPLEX:数値の組を複素数に変換
COMPLEX関数は2つの数値を虚数単位で結びつけて複素数に変換します。COMPLEX関数は
=COMPLEX(実数部,虚数部,[単位])
という形で入力します。たとえば
=COMPLEX(1,3)
と記述すると「1+3i」という文字列に変換されます。[単位] は「i」または「j」のどちらかを指定しますが、省略すると「i」を指定したことになります。
IMREAL:複素数の実部
IMREAL関数は複素数から実部 (real part) を抜き出します。IMREAL関数は
=IMREAL(複素数)
の形で入力し、引数には「”a+bi”」もしくは「”a+bj”」で表された複素数を指定します。たとえば
=IMREAL("5+3i")
と入力すると、複素数 5 + 3i の実数部「5」が戻ってきます。あるいは COMPLEX 関数をネストして
=IMREAL(COMPLEX(5,3))
としても、やはり「5」を返します。
IMAGINARY:複素数の虚部
IMAGINARY関数は複素数から虚部 (imaginary part) を抜き出します。IMAGINARY関数は
=IMAGINARY(複素数)
の形で入力し、引数には「”a+bi”」あるいは「”a+bj”」で表された複素数を指定します。たとえば
=IMAGINARY("7+9i")
と入力すると、複素数 7 + 9i の虚数部「 9 」が戻ってきます。あるいは COMPLEX 関数を入れ子にして
=IMAGINARY(COMPLEX(7,9))
としても、やはり虚数部「 9 」を返します。
IMCONJUGATE:共役複素数
複素数 a + bi に対して a – bi を共役複素数とよびます。IMCONJUGATE関数は
=IMCONJUGATE(複素数)
と入力して引数の共役複素数を返します。たとえば
=IMCONJUGATE("1+2i")
と入力すると 1+2i の共役複素数「1-2i」を返します。
IMABS:複素数の絶対値
複素数 a + bi を複素数平面上の点 (a, b) 上の点に対応させたとき、原点から (a, b) までの距離が複素数の絶対値と定義されています。IMABS関数は
=IMABS(複素数)
と入力し、引数の絶対値を返します。たとえば
=IMABS("1+i")
と入力すると、√2 の近似値「1.414214」が返されます。
IMARGUMENT:複素数の偏角
複素数 a + bi を複素数平面上の点 (a, b) 上の点に対応させたとき、原点と (a, b) を結ぶ線分が実軸となす角度 θ が偏角と定義されています。IMARGUMENT関数は
=IMARGUMENT(複素数)
という形式で入力し、複素数の偏角 θ をラジアン単位で得ます。たとえば
=IMARGUMENT("1+1i")
と入力すると π/4 の近似値「0.785」が返ります。DEGREES 関数を用いて
=DEGREES(IMARGUMENT("1+1i"))
と入力すれば度数法単位で「 45 」を得ることができます。
IMSUM:複素数の和
IMSUM関数は
=IMSUM(複素数1[,複素数2,...])
と入力し、引数に指定した全ての複素数の総和を計算します。たとえば
=IMSUM("2+i","1+3i")
と入力すると「3+4i」が返ります。あるいは
=IMSUM(COMPLEX(2,1),COMPLEX(1,3))
と入力しても同じ結果を得ることができます。
IMSUB:複素数の差
IMSUB関数は
=IMSUB("複素数1","複素数2")
の形で入力し、複素数 1 から複素数 2 を引いた複素数を返します。たとえば
=IMSUB("8+7i","2+3i")
と入力すると「6+4i」が返ります。あるいは
=IMSUB(COMPLEX(8,7),COMPLEX(2,3))
と入力しても同じ結果になります。
IMPRODUCT:複素数の積
IMPRODUCT関数は
=IMPRODUCT(複素数1[,複素数2, ...])
と入力し、指定した引数の積を返します。たとえば
=IMPRODUCT("5+2i","1+3i")
とすると、5 + 2i と 1 + 3i の積「 -1 + 17i 」を返します。
IMDIV:複素数の商
IMDIV関数は
=IMDIV("複素数1","複素数2")
の形で入力し、複素数1 を複素数2 で割った値を返します。たとえば
=IMDIV("5+2i","1+i")
と入力すると複素数 5 + 2i を複素数 1 + i で割った「3.5-1.5i」を返します。
IMPOWER:複素数のべき乗
IMPOWER関数は
=IMPOWER(複素数,数値)
の形式で記述し、1 つめの引数を底、2 つめの引数を指数とするべき乗を返します。たとえば
=IMPOWER("1+i",5)
と入力すると (1 + i)5 を計算して「-4-4i」という文字列を得ることができます。
IMSQRT:複素数の平方根
IMSQRT関数は
=IMSQRT(複素数)
と入力して引数の平方根、すなわち引数を 0.5 乗した複素数を返します。たとえば
=IMSQRT("3+4i")
と入力すると (3+4i)0.5 を計算して「2+i」を得ます。

エクセルや数学に関するコメントをお寄せください