この記事では VBA でモンテカルロ法(Monte Carlo method)を実装して、円周率の近似値や定積分を求める方法を解説します。
【VBA】モンテカルロ法による円周率の計算
下の図のように半径 $1$ の四分円と、それに外接する正方形を考えます。
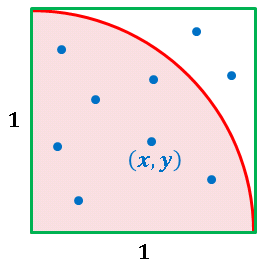
そして、この正方形の中に無作為に点を $N$ 回発生させます。そのうちの何割かは四分円の中に入ることになります。その総数を $N_c$ とします。$N_c$ と $N$ の比は、四分円の面積 $S_c$ と正方形の面積 $S$ の比にほぼ等しくなっているはずだと考えます。つまり
\[\frac{N_c}{N}=\frac{\pi}{4}\]
なので、円周率は
\[\pi=4\frac{N_c}{N}\]
と計算できるはずです。$N$ を大きくするほど近似の精度は良くなります。とりあえず $N$ を $100000$ と設定して計算してみましょう。
'[VBA] モンテカルロ法による円周率の近似計算 Sub Monte_Carlo_Pi() Dim x As Double, y As Double Dim r As Double, p As Double Dim n As Long, nc As Long Randomize For n = 1 To 100000 '無作為な点(x,y)を1つ生成 x = RND y = RND '原点からの距離の2乗を計算 r = x ^ 2 + y ^ 2 '原点からの距離が 1 以内ならば '四分円に入ったカウント数に1を加える If r <= 1 Then nc = nc + 1 End If Next n '円周率の近似値を計算 p = 4 * nc / n Debug.Print p End Sub
Monte_Carlo_Pi() を実行するとイミディエイトウィンドウに円周率の近似値が表示されます。乱数を使っているので、実行する度に違った値となります。
Monte_Carlo_Pi() の構造について簡単に解説します。$n$ は無作為な点の発生回数なので、For…Next ステートメントのカウンタ変数の上限値となっています。Monte_Carlo_Pi() では
For n = 1 To 100000
としてあるので、上限値を 100,000 としてありますが、より高い精度を求めるのであれば、この上限値を書き換えてください。x と y に 0 から 1 の乱数を入れていますが、これが発生した点の座標 (x, y) となっています。
r <= x ^ 2 + y ^ 2
という記述で (x, y) の原点からの距離の2乗を変数 r に入れます。
If r <= 1 Then
は r が 1 以内であること、つまり点が四分円の中にあるという条件で、それが満たされた場合に限って
nc = nc + 1
として四分円に入ったカウント数 nc に 1 を加えます。最後に nc と n の比率を使って
p = 4 * nc / n
として円周率の近似値を p に入れています。
【VBA】モンテカルロ法による定積分の計算
関数 $f(x)=x^2$ の定積分
\[I=\int_{0}^{a}x^2dx\]
をモンテカルロ法で計算してみます。

図にある面積 $a\times a^2=a^3$ の長方形の中にランダムな点 $(x,\:y)$ を $N$ 個発生させて、そのうち黄色の網掛け部分、すなわち
\[y\leq f(x)\]
に入った回数が $n$ 回であったとすると、
\[I=\int_{0}^{a}x^2dx\simeq\frac{n}{N}a^3\]
というように近似計算できます。モンテカルロ法による定積分の計算プログラムの一例を載せておきます。
'[VBA] モンテカルロ法による定積分の計算 Sub MonteCarlo_Integral() Dim x As Double, y As Double Dim a As Double, itg As Double Dim n As Long, k As Long, ct As Long '積分の上限値 a = 3 Randomize '試行回数の設定 n = 1000 For k = 1 To n '無作為点(x,y)を生成 x = a * RND y = a ^ 2 * RND 'y < f(x) ならば If y < x ^ 2 Then 'カウント数に 1 を加える ct = ct + 1 End If Next k '積分近似値を計算します itg = ct * a ^ 3 / n Debug.Print itg End Sub
真値 (9) と比較しやすいように、上限を $a=3$ としてあります。試行回数は $N=10^3$ です。マクロを実行すると 9 の近傍値が現れるはずです。$N$ の値を大きくするほど精度は上がりますが、そのぶん処理に時間がかかります。$N=10^5$ でも 3 桁ほどの精度しかないので、定積分をわざわざこの手法で行うメリットはありませんが(シンプソンの公式など他にいくらでも有用な方法があります)、モンテカルロ法は色々な分野のシミュレーションに応用がきくので、そのアルゴリズムを知っておいて損はありません。
エクセルや数学に関するコメントをお寄せください