【VBA】シンプソンの公式

この記事の前半では、シンプソンの公式で数値積分する方法を解説します。後半では、VBA で同原理に基づくプログラム Simpson_Integral() を実装し、具体的な計算を行なってみます。

シンプソンの公式（Simpson’s rule）

ある曲線上の 3 点
\[(\alpha,\:f_0),\quad \left(\frac{\alpha+\beta}{2},\:f_1\right),\quad (\beta,\:f_2)\]
を通る放物線と $x=a,\:x=b$ および $x$ 軸とで囲まれる面積を求めてみます。

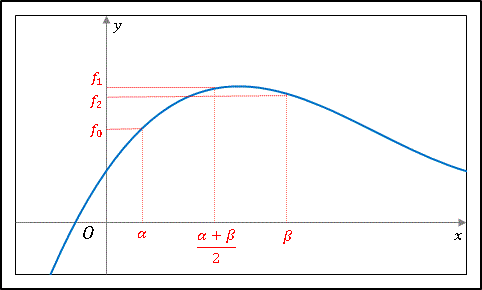
放物線を $y=Ax^2+Bx+C$ とおいて面積を計算すると
\[s=\int_{\alpha}^{\beta}(Ax^2+Bx+C)dx=\frac{A}{3}(\beta^3-\alpha^3)+\frac{B}{2}(\beta^2-\alpha^2)+C(\beta-\alpha)\]
$\beta^3-\alpha^3$ を因数分解すると
\[\beta^3-\alpha^3=(\beta-\alpha)(\alpha^2+\alpha\beta+\beta^2)\]
となるので、式を整理すると
\[s=\frac{\beta-\alpha}{3}\left\{ A(\alpha^2+\alpha\ \beta+\beta^2)+\frac{3B}{2}(\alpha+\beta)+3C \right\}\]
となります。放物線は
\[(\alpha,\:f_0),\quad \left(\frac{\alpha+\beta}{2},\:f_1\right),\quad (\beta,\:f_2)\]
を通るので、
\[\begin{align*}f_0&=A\alpha^2+B\alpha+C\\[6pt]f_1&=A\left( \frac{\alpha+\beta}{2} \right) ^2+B \left( \frac{\alpha+\beta}{2} \right) +C\\[6pt]f_2&=A\beta^2+B\beta+C\end{align*}\]
が成り立ちます。そこで $f_0+4f_1+f_2$ を計算してみると
\[f_0+4f_1+f_2=2\left\{ A(\alpha^2+\alpha\ \beta+\beta^2)+\frac{3B}{2}(\alpha+\beta)+3C\right\}\]
となっていることがわかります。よって面積は
\[s=\frac{\beta-\alpha}{6}(f_0+4f_1+f_2)\]
と計算できます。今度は下図のように曲線の区間 $[a,\:b]$ の面積を $2m$ 個の帯に分割して曲線上の点 $P_0,\:P_1,\:P_2,\:\cdots,\:P_{2m-2},\:P_{2m-1},\:P_{2m}$ とします。

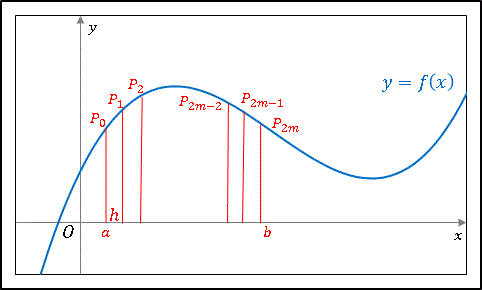
1 区分の幅は
\[h=\frac{b-a}{2m}\]
で与えられます。そして帯を 2 個ずつまとめて
\[P_0P_1P_2,\:P_2P_3P_4,\:P_4P_5P_6,\:\cdots\]
という弧をもつ $m$ 個の帯をつくります。区間 $[a,\:b]$ において、曲線 $y=f(x)$ と $x=a,\:x=b$ および $x$ 軸に囲まれる面積を
\[S=\int_{a}^{b}S(x)dx\]
とおいて、それぞれの帯の面積に先ほどの放物線近似を適用すると
\[S=\frac{h}{3}\sum_{k=0}^{m-1}\left[f(a+2kh)+4f(a+(2k+1)h)+f(a+(2k+2)h)\right]\]
となります。これがシンプソンの公式とよばれる積分近似式です。

シンプソンの公式を使って、有名なガウス積分
\[\int_{a}^{b}\exp (-x^2)dx\]
を計算するプロシージャを載せておきます。

'[VBA]シンプソンの公式によるガウス積分の近似計算

Sub Simpson_Integral()
　　Dim a As Double, b As Double
　　Dim h As Double, s As Double
　　Dim m As Integer, k As Integer

　　'区間[a,b]の入力を促します
　　a = Application.InputBox("左端を入力してください", Type:=1)
　　b = Application.InputBox("右端を入力してください", Type:=1)

　　If a > b Then
　　　　MsgBox "数値が正しくありません"
　　Exit Sub

　　Else

　　　　'mを指定
　　　　m = 10

　　　　'1 区分の長さ
　　　　h = (b - a) / (2 * m)

　　　　'帯を足し合わせる
　　　　For k = 0 To m - 1
　　　　　　s = s + exp(-(a + 2 * k * h) ^ 2) _
　　　　　　+ 4 * exp(-(a + (2 * k + 1) * h) ^ 2) _
　　　　　　+ exp(-(a + (2 * k + 2) * h) ^ 2)
　　　　Next k

　　　　s = s * h / 3

　　　　MsgBox s

　　End If

End Sub

Simpson_Integral() を実行すると端点 $a$ と $b$ を入力するように促されますので、たとえば $a=0,\:b=1$ としてみると 0.74682 という値が返ってきます。