【Excel】POISSON.DISTでポアソン分布を生成する

平均値を一定に保った二項分布の様子

下の図は平均値 $\mu=np=2$ を維持したまま試行回数 $n$ と成功率 $p$ を変化させた二項分布 $\mathrm{Bin}(n,p)$ の確率密度のグラフです。
 

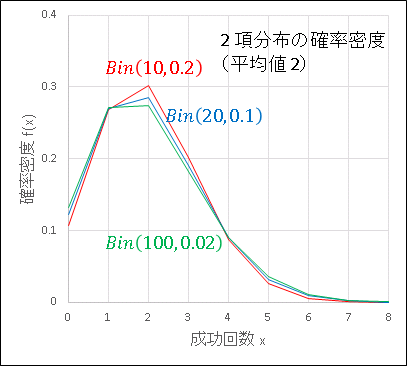
3 つのグラフはほとんど重なっていて、似たような分布をしていることがわかります。成功率 2 % の試行を 10 回繰り返すことと、成功率 1 % の試行を 20 回繰り返すことは、平均値 2 の周囲にほぼ同じ分布が広がるであろうことは直感にも一致しています。

ポアソン分布

このように平均値 $\mu=np$ を一定に保ちながら $n\rightarrow \infty$ の極限をとると ($n$ を大きくしたぶん、同時に $p$ も小さくしなければなりません) 、 二項分布の分布曲線は ポアソン分布 (Poisson distribution) と呼ばれる
 \[f(x)=\frac{\mu^x}{x!}e^{-x}\tag{A}\]\[\sigma^2=\mu,\quad \sigma=\sqrt{\mu}\]
に近づいていきます。もちろん現実問題では試行回数を無限大にすることはできませんが、$n$ を十分に大きくとると、ほぼこの曲線にのるということです。

【ポアソン分布の証明】二項分布の確率密度は
 \[f(x)={}_n\mathrm{C}_x\:p^x(1-p)^{n-x}\]
で与えられます。平均値は $\mu=np$ なので
 \[\begin{align*}f(x)&=\frac{n(n-1)\cdots [n-(x-1)]}{x!}\left(\frac{\mu}{n}\right)^x\left( 1-\frac{\mu}{n}\right)^{n-x}\\[6pt]&=\frac{\mu^x}{x!}\left( 1-\frac{1}{n}\right)\left( 1-\frac{2}{n}\right)\cdots\left( 1-\frac{x-1}{n}\right)\left\{ \left( 1-\frac{\mu}{n}\right)^{-n/\mu}\right\}^{-\mu}\left( 1-\frac{\mu}{n}\right)^{-x}\end{align*}\]
ここで $-n/\mu=t$ とおくと、$n\rightarrow \infty$ としたとき、$t\rightarrow -\infty$ なので
 \[\lim_{n\rightarrow \infty}\left( 1-\frac{\mu}{n}\right)^{-n/\mu}=\lim_{t\rightarrow -\infty}\left( 1+\frac{1}{t}\right)^t=e\]
となり、ポアソン分布
 \[f(x)=\frac{\mu^x}{x!}e^{-x}\tag{A}\]
が得られます。ポアソン分布は発生確率 $p$ が非常に小さい事象（交通事故の発生回数など）に対して良い近似値を与えます。

ポアソン分布の分散と標準偏差

二項分布の分散は
 \[\sigma^2=np(1-p)=\mu\left( 1-\frac{\mu}{n}\right)\]
で与えられるので、$n\rightarrow \infty$ の極限をとれば $\sigma^2=\mu$ となって平均に等しいことがわかります。また標準偏差は $\sigma=\sqrt{\mu}$ となります。

【Excel】POISSON.DIST関数

Excel には $x$ と $\mu$ を与えてポアソン分布にしたがう確率値を返す POISSON.DIST関数 が用意されています（Excel 2007 以前のバージョンでは POISSON関数）。

=POISSON.DIST(x,μ,関数形式)

3 つめの引数（関数形式）を 0 あるいは FALSE に指定すると確率密度 $f(x)$、1 または TRUE を指定すると累積分布 $F(x)$ を返します。この関数を用いてポアソン分布の確率密度のグラフを描くと次のようになります。
 

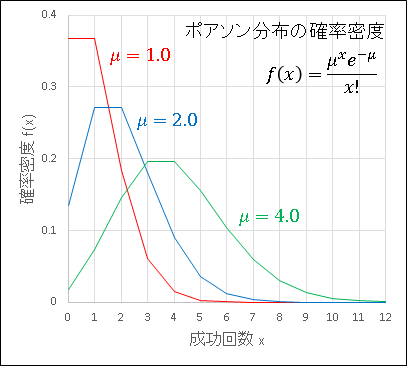
平均値 $\mu$ の増加にともなって、グラフは幅を広げながら右下へ移動します。試行回数 $n$ は無限にとっているのに、実現回数は数回程度であることがわかります。また累積分布関数は下図のようになります。
 

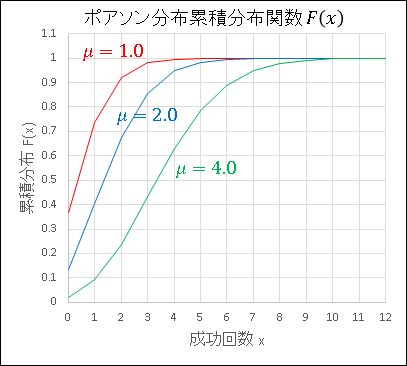
たとえば平均が $\mu=4.0$ であれば、$X\leq3$ である確率は約 40%, $X\leq5$ である確率は約 80% となります。