高次不等式の解き方

式の中に含まれる項のうち、最大次数が $n$ であるような不等式のことを高次不等式（inequality of higher degree）とよびます。以下で色々な高次不等式の解き方を解説します。

二次不等式

二次不等式を解くことは、一次不等式に比べてずっと難しく、二次関数や因数分解などの知識が必要です。例として
 \[x^2-3x+2\lt 0\tag{1}\]
という不等式を解いてみます。

グラフを使って二次不等式を解く

最初に二次関数のグラフを使った解き方を見てみましょう。与えられた不等式
 \[x^2-3x+2\lt 0\tag{1}\]
の右辺を $y$ とおき、$y=x^2-3x+2$ のグラフを描いてみると下の図のようになります（不等式を解くときは $x$ 軸との交点だけわかれば十分です）。
 

 
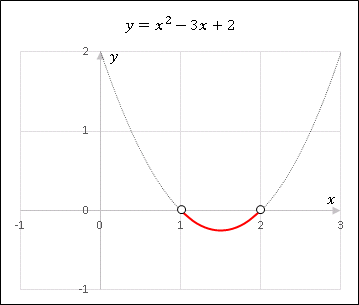
このグラフで $x^2-1$ が 負となる $x$ の範囲（赤い部分）を見ると
 \[1\lt x \lt 2\]
となっているので、これが (1) の解となります。

因数分解を使って二次不等式を解く

今度は同じ不等式を因数分解を使って解いてみます。
 \[x^2-3x+2\lt 0\tag{1}\]
の左辺を因数分解すると
 \[(x-1)(x-2)\lt 0\]
となります。ここで「2 つの数字の積が負になるのは、片方が正で片方が負になるときだけ」と考えます。
 
① まず最初に
 \[x-1\lt 0\quad かつ\quad x-2\gt 0\]
の場合を考えてみます。不等式を変形して
 \[x\lt 1\quad かつ \quad x\gt 2\]
となりますが、「$1$ より小さく $2$ より大きい」数など存在しないので、このケースは除外します。次に
\[x-1\gt 0\quad かつ\quad x-2\lt 0\]
を考えます。不等式を変形して
\[x\gt 1\quad　かつ\quad x\lt 2\]
となります。つまり $x$ のとりうる範囲は
 \[1\lt x\lt 2\]
となります。

三次不等式

今度は三次不等式
 \[x^3-2x^2-x+2\leq 0\tag{2}\]
を解いてみます。
 \[f(x)=x^3-2x^2-x+2\]
とおいて、$f(x)$ に $1,\:-1,\:2$ を代入してみると、
 \[f(1)=0,\quad f(-1)=0,\:\quad f(2)=0\]
となるので、$f(x)$ は $1,\:-1,\:2$ を因数にもちます。すなわち、
 \[f(x)=(x+1)(x-1)(x-2)\]
と因数分解できます。不等式は
 \[(x+1)(x-1)(x-2)\leq 0\]
となります。3 数の積が負となるのは「全てが負数、あるいはどれか 1 つが負数」なので、そうしたケースを１つ１つチェックしながら解くこともできますが、相当に手間がかかります。ここでは微積分を用いて解いてみます。$f(x)$ の因数分解により、$y=f(x)$ のグラフは $x=-1,\:1,\:2$ で $x$ 軸と交わることがすでにわかっています。次はグラフの凹凸を調べます。$f(x)$ を微分すると
 \[f'(x)=3x^2-4x-1\]
$f'(x)=0$ とおいて判別式を計算してみると
 \[\frac{D}{4}=7\gt 0\]
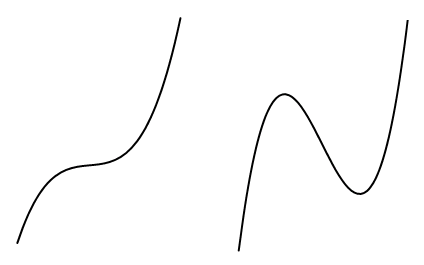
なので、$f'(x)=0$ は 2 つの実数解をもちます。つまり接線の傾きが $0$ になるところが 2 つあります。一般には、これだけでその 2 点で極値をとるとは断定できませんが、3 次関数の場合は $x^3$ の係数が正のとき、グラフの概形が以下の 2 種類しかないので、$f'(x)=0$ となる点が 2 つあれば極大値と極小値が存在します。
 

$x$ 軸を 3 回横切っているので、左の極大値は正、右の極小値は負の値をとります。下図の黒い点線が $y=f(x)$ のグラフ、赤い部分が $f(x)$ が負となる範囲です。
 

 
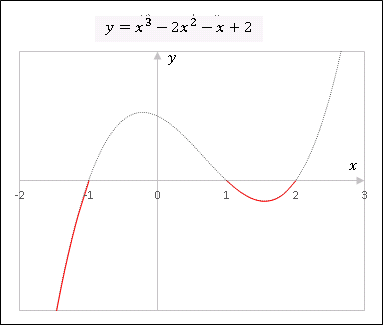
したがって、不等式を満たす $x$ の範囲は
 \[x\leq-1,\quad 1\leq x\leq 2\]
となります。

高次不等式の例題と解説

高次不等式には $x^2$ や $x^3$ といった一変数のみならず、$xy$ や $xyz$ の項を含む多変数のものもあります。

【例題】$3$ つの変数 $x,\:y,\:z$ について
\[|x|\lt 1,\:|y|\lt 1,\:|z|\lt 1\]のように範囲を制限します。
(1) 不等式 $xy+1\gt x+y$ が成り立つことを証明してください。
(2) (1) の結果を用いて $xyz+2\gt x+y+z$ が成り立つことを証明してください。

【解答】$A\gt B$ は $A-B\gt 0$ です。
(1) $xy+1\gt x+y$ の左辺から右辺をひくと
 \[\begin{align*}xy+1-(x+y)\,&=x(y-1)-(y-1)\\[6pt]&=(x-1)(y-1)\end{align*}\]
となります。$|x|\lt 1,\:|y|\lt 1$ より、$x$ と $y$ は $1$ より小さな数なので、
 \[(x-1)(y-1)\gt 0\]
となります。等号成立は $x=1$ または $y=1$ のときです。

(2) (1) で証明した不等式を用いると、$x$ と $yz$ について
 \[x(yz)+1\gt x+yz\]
が成立します。両辺に $1$ を加えると
 \[x(yz)+2\gt x+yz+1\tag{*}\]
ここで再び (1) の不等式より、$y$ と $z$ について
 \[yz+1\gt y+z\]
が成り立つので、(*) に代入すると
 \[xyz+2\gt x+y+z\]
が成り立ちます。

【補足】(1) で証明した不等式 $xy+1\gt x+y$ において、$\displaystyle x=\frac{99}{100},\:y=\frac{1}{2}$ として左辺と右辺の差を計算してみると、
 \[\begin{align*}xy+1=\frac{299}{100}\\[6pt]x+y=\frac{298}{100}\end{align*}\]
その差は僅かに $\displaystyle x=\frac{1}{100}$ となって、ぎりぎりのところで不等式が成立しています。これは (1) の不等式において $x$ あるいは $y$ を極限まで $1$ に近づけると両辺の差は限り無く小さくなることからもわかります。このように、ぎりぎりのところで大小を評価できる不等式ほど数学的に価値が高いといえます。