【Excel】NORMDIST

正規分布

正規分布の確率密度関数

正規分布（normal distribution）とは
 \[f(x)=\frac{1}{\sqrt{2\pi}\sigma }\exp\left\{-\frac{(x-\mu)^2}{2\sigma ^2} \right\}\]
で定義される確率分布のことです。ここに $\mu$ は平均値、$\sigma$ は標準偏差であり、その分布を $N(\mu,\sigma)$ で表します。平均値を $\mu=4$ に固定して、標準偏差 $\sigma=1, 2$ という２つの曲線を重ねてみます。
 

 
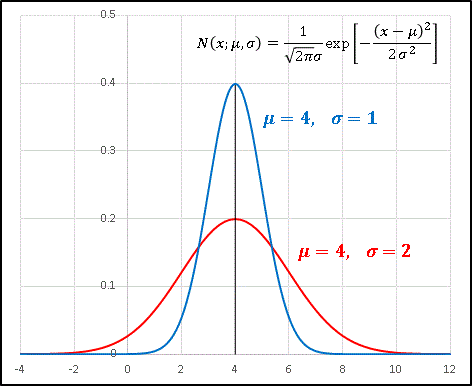
どちらも平均値 $\mu=4$ で最大値をとり、左右対称に裾野が広がっています。これは $x$ が $\mu=4$ をとる確率が最も高く、そこから値がずれてゆくほどその確率が減少していくということです。人間の身長や体重であるとか、大勢の人が受験した試験の点数などは近似的にこの正規分布にしたがうことが知られています。また上のグラフを見ると $\sigma$ が何を意味しているか明らかです。$\sigma=1$ の曲線は $\sigma=2$ の曲線に比べて幅が狭く、ほとんどの場合（つまりかなりの確率で）、$x$ が $2$ から $6$ の間に入ってしまいます。つまり、標準偏差 $\sigma$ は値のばらつき具合を示していて、$\sigma$ が大きいほど中央値からずれる確率が大きいということです。ちなみに、$exp(-ax^2)$ のような形の関数を ガウス関数 とよびます。

正規分布の累積分布関数

正規分布曲線を $-\infty$ から $x$ まで積分した
 \[F(x)=\frac{1}{\sqrt{2\pi }\sigma }\int_{-\infty}^{x}\exp \left \{ -\frac{(x-\mu )^2}{2\sigma ^2} \right \}dx\]
を正規分布の累積分布関数とよび、確率変数が $x$ 以下の値をとる確率を表します。
 

 
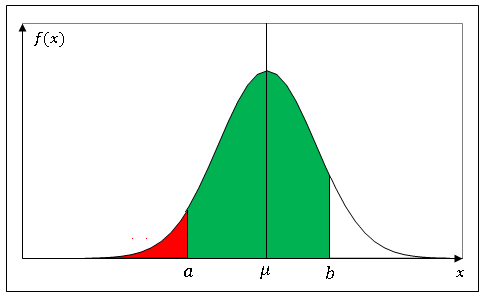
上図において赤い部分の面積は $f(x)$ を $-\infty$ から $a$ まで積分した値 $F(a)$ に相当します。また赤い部分と緑色の部分を足し合わせた面積は $F(b)$ です。したがって、変数 $X$ が $a$ から $b$ までの値をとる確率は
 \[P(a\leq X\leq b)=F(b)-F(a)\]
で与えられることになります。正規分布の累積分布関数 F(x) は初等関数で表すことはできませんが、Excel では後述する NORM.DIST関数によって簡単に計算することができます。

標準正規分布

平均値 $\mu$, 標準偏差 $\sigma$ にしたがう正規分布
 \[f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\frac{(x-\mu)^2}{2\sigma ^2}\right\}\]
において確率変数を
 \[Z=\frac{X-\mu}{\sigma}\]
のように変換したとき（標準化変換）、変数 $Z$ は
 \[f(z)=\frac{1}{\sqrt{2\pi }\sigma }\exp\left( -\frac{z^2}{2}\right)\]
という平均 $0$, 標準偏差 $1$ の正規分布 $N(0,1)$ に従います。このような分布のことを標準正規分布といい、そのグラフは $x=0$ について左右対称となります。
 

 
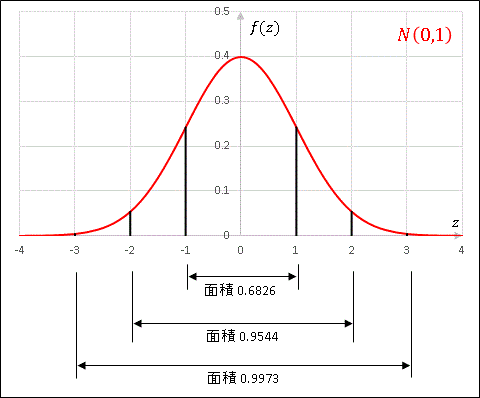
すると $-1\leq Z\leq 1$ となる確率は
 \[P(-1\leq Z\leq 1)=F(1)-F(-1)=0.682\]
と計算されます。確率変数を X に戻すと
 \[P(\mu-\sigma\leq Z\leq\mu+\sigma)=0.682\]
となります。これは平均のまわりに $\sigma$ の幅をとったとき、変数がその内側にある確率が約 60% であることを示しています。同様に
 \[\begin{align*}P(\mu-2\sigma\leq Z\leq\mu+2\sigma)=0.954\\[6pt]
P(\mu-3\sigma\leq Z\leq\mu+3\sigma)=0.977\end{align*}\]
と計算されます。
 

 
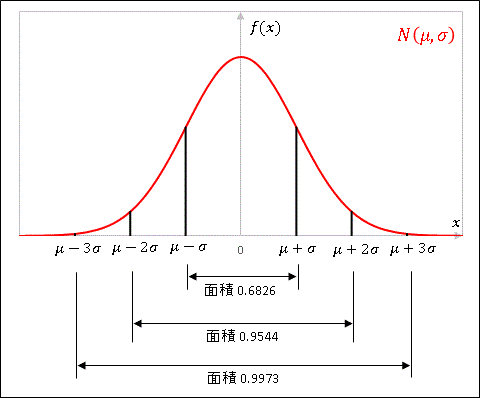
つまり変数のほとんど全て (98%) が平均から $\pm\sigma$ の範囲にあるということです。

【Excel】正規分布と累積分布関数

Excel には正規分布と累積分布を計算するために

NORM.DIST(x,平均,標準偏差,関数形式)

という関数が用意されています（2007 以前のバージョンでは NORMDIST関数）。４つめの引数によって、正規分布（関数形式=0）か累積分布関数（関数形式=1）を選ぶことができます。たとえば、ある試験が実施されて平均が $60$ 点、標準偏差が $15$ であったとき、点数が $50$ 点から $70$ 点であった受験生の割合は

=NORM.DIST(70,60,15,1)-NORM.DIST(50,60,15,1)

によって計算できます。その値は 0.495 なので、受験生の約半数がこの範囲内に収まっていることがわかります。また Excel には標準正規分布を計算する

NORM.S.DIST(x,関数形式)

も用意されています。変数が $\sigma$ 以内に入っている確率は

=NORM.S.DIST(1,1)-NORM.S.DIST(-1,1)

によって計算できます。0.6827 という値が返ってくるはずです。