素数の原始根

素数の原始根

　位数について復習しておきます。位数とは
　
\[a^k\equiv 1\quad (\mathrm{mod}\:m)\]
となるような最小の正整数 $k$ であり、
　
\[k=\mathrm{ord}_m(a)\]
と表しました。ここで素数 $p$ についてはフェルマーの小定理
　
\[a^{p-1}\equiv 1\quad (\mathrm{mod}\:p)\]
が成り立っています。このとき、もし $p-1$ が上の合同式を満たす最小のベキ指数であるならば、位数は $p-1$ となります。このような条件を満たす正整数 $a=g$ を $p$ の 原始根 (primitive root) とよびます：
　
\[p-1=\mathrm{ord}_p(g)\]
　すなわち原始根 $g$ とは $g^1,\;g^2,\;\cdots$ とべき乗をつくっていったときに、ベキ指数が $p-1$ のときに初めて
　
\[g^{p-1}\equiv 1\quad (\mathrm{mod}\:p)\]
となるような正整数のことです。

　たとえば $p=7$ においては $p-1=6$ 乗で初めて $1$ と合同になる数が原始根です。具体的に調べてみると ……
　
\[\begin{align*}&3^1\equiv 3&\quad (\mathrm{mod}\:7)\\[6pt]
&3^2\equiv 9\equiv 2&\quad (\mathrm{mod}\:7)\\[6pt]&3^3\equiv 6&\quad (\mathrm{mod}\:7)\\[6pt]
&3^4\equiv 18\equiv 4&\quad (\mathrm{mod}\:7)\\[6pt]&3^5\equiv 12\equiv 5&\quad (\mathrm{mod}\:7)\\[6pt]
&3^6\equiv 15\equiv 1&\quad (\mathrm{mod}\:7)\end{align*}\]
となるので $3$ は $7$ の原始根です。また、
　
\[\begin{align*}&5^1\equiv 5&\quad (\mathrm{mod}\:7)\\[6pt]
&5^2\equiv 25\equiv 4&\quad (\mathrm{mod}\:7)\\[6pt]
&5^3\equiv 20\equiv 6&\quad (\mathrm{mod}\:7)\\[6pt]
&5^4\equiv 30\equiv 2&\quad (\mathrm{mod}\:7)\\[6pt]
&5^5\equiv 10\equiv 3&\quad (\mathrm{mod}\:7)\\[6pt]
&5^6\equiv 15\equiv 1&\quad (\mathrm{mod}\:7)\end{align*}\]
となるので $5$ も $7$ の原始根です。このように原始根は複数存在することもあります。そうすると、$g=3,\;5$ で原始根を取りつくしたかどうか心配になりますが、ここで前回学んだ 定理 E5 を参照します：

　今は $p-1$ の最大の約数である $p-1$ を考えればいいので、

　$p=7$ のときは
　
\[\varphi(6)=\varphi(2)\varphi(3)=1\cdot 2=2\]
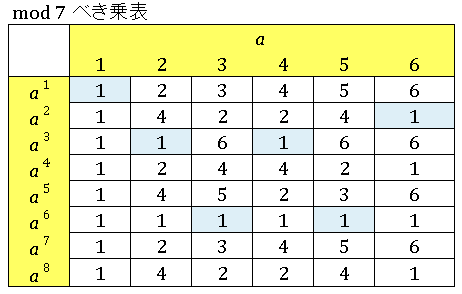
なので全部で 2 個です。つまり $g=3,\;5$ で原始根を取りつくしていることがわかります。素数 $\mathrm{mod}\:7$ のベキ乗表でも、これ以外に原始根が存在しないことを確認しておいてください。

原始根の一般的な定義

　必ずしも素数ではない $m$ について、原始根を次のように定義します。

　すなわち $m$ の原始根とは、ベキ乗して $\varphi(m)$ で初めて
　
\[g^{\varphi(m)}\equiv 1\quad (\mathrm{mod}\:p)\]
となるような正整数 $g$ のことです。ただし本講座では当面の間は素数の原始根を扱いますので、一般の原始根についてはあまり気にする必要はありません。