【Excel】行列と逆行列

【Excel】行列と逆行列の演算

Excel には複数のセルに入力された数値をまとめて取り扱う 配列という概念があります。ちょっとややこしいのですが、Excel の配列と数学の行列は異なるものです。しかし、演算の一部は両者で共通しています。また配列同士を行列と同じように演算する数学関数も用意されているので、配列を使って数学の行列を計算できます。今回は配列同士の足し算を学びます。配列の足し算は行列の足し算と同じ演算なので、数学関数を使わずに普通の「+」という演算子で扱うことができます。

【Excel】行列の和と差

それでは次のような行列 A, B に対応する配列を入力してみます。
 \[A=\begin{pmatrix}1&2\\3&4\end{pmatrix},\quad B=\begin{pmatrix}1&1\\2&2\end{pmatrix}\]
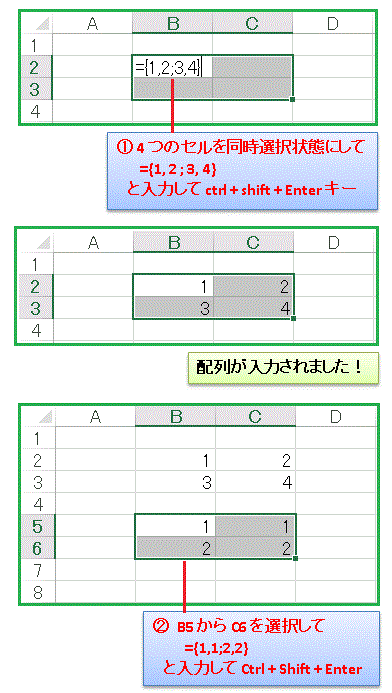
4 つのセルに別々に数値を入力してもいいのですが、少しだけ便利な方法があります。下図にあるように、セル B2 から C3 を同時選択状態にしておいてから、

={1,2;3,4}

というように入力します。上の行と下の行を「 ; 」で区切っていると覚えるようにしてください。上の式もいわゆる 配列数式 の１つです。この配列数式をシートに反映させるためには、普通に Enter を押してはいけません。

Ctrl + Shift + Enter

という 3 つのキー同時押しが必要なのです。どうしてこのような仕様になっているのかはわかりませんが、配列数式を扱うときは我慢するしかありません。同じように B5 から C6 を選択して

={1,1;2,2}

と入力して Ctrl + Shift + Enter を押して行列 B を作ります。下の図で流れを確認してください。
 

それでは、セル B8 から C9 に行列 A + B を計算してみましょう。セル B8 から C9 を同時選択してまず「=」だけを入力します。そしてマウスを上のほうに持って行って、B2 から C3 を選択します。次に「+」と入力し、B5 から C6 を選択して [Ctrl] + [Shift] + [Enter] です。
 

 
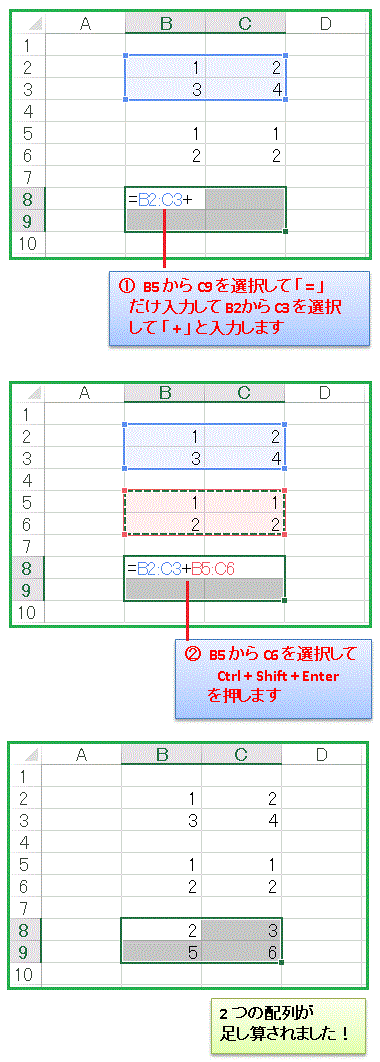
行列の成分同士が足し算されていますね。

【Excel】行列積

行列 $A$ と行列 $B$ を
 \[A=\begin{pmatrix}a&b\\c&d\end{pmatrix},\quad B=\begin{pmatrix}e&f\\g& h\end{pmatrix}\]
とおくと、行列の積 $AB$ は次のように定義されます。
 \[AB=\begin{pmatrix}a&b\\c&d\end{pmatrix}\begin{pmatrix}e&f\\g&h\end{pmatrix}=\begin{pmatrix}ae+bg&af+bh\\ce+dg&cf+dh\end{pmatrix}\]
Excel には行列積を計算する関数

=MMULT(配列1, 配列2)

が用意されています (MMULT は Matrix Multiplication の略です)。

次のような行列 A, B に対応する配列を入力してみます。
 \[A=\begin{pmatrix}1&3\\5&2\end{pmatrix},\quad B=\begin{pmatrix}2&4\\1&3\end{pmatrix}\]
先程と同じように

={1,3;5,2}

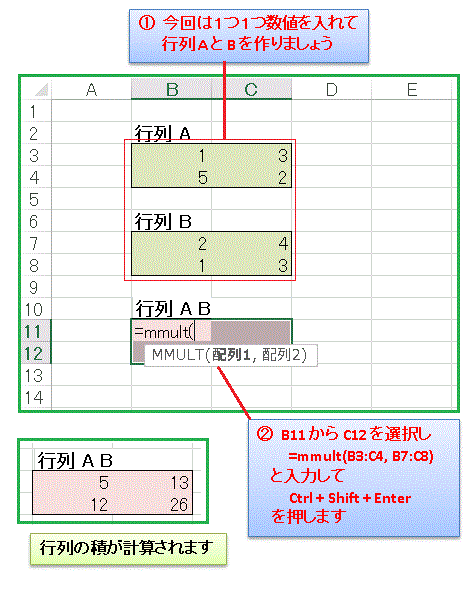
としてもよいのですが、実はこの入力方法で行列を作ると、配列がひとかたまりとして扱われるようになり、あとで数値を変更できないという問題点があります（正確に言うと、できないことはないけど、変更するのがとても面倒なのです）。もちろん行列の成分を変えるつもりが一切ないのなら、この方法で構わないのですが、行列の数値を可変データにしたい場合には困ることになります。その時々に応じて使い分けてください。今回は下図を参照にしながらセルに数値を１つ１つ数値を入力しておきましょう。行列の入力を終えたら MMULT で行列の積 AB を計算します。セル B11 から C12 を同時選択状態にしておいてから、

=MMULT(B3:C4,B7:C8)

と入力し、Ctrl + Shift + Enter を押して計算を実行します。範囲を指定する「 B3:C4 」と「 B7:C8 」のところはマウスを動かしてセル B3 から C4（行列 A に相当する範囲）と、セル B7 から C8 まで（行列 B に相当する範囲）を選択すると楽です。
 

今回のシートは 2 行 2 列に限れば、あらゆる行列の積を計算できますから、フォルダの片隅にでも残しておくと便利だと思います。数値を色々と変えて試してみてくださいね。次回は逆行列の求め方を学びます。

【Excel】逆行列

ある行列 $A$ に対して
 \[AA^{-1}=A^{-1}A=I\]
となるような行列 $A^{-1}$ が存在するとき（存在しないこともあります）、行列 $A^{-1}$ を $A$ の逆行列と定義します。$A$ が 2 行 2 列の行列であり、
 \[A=\begin{pmatrix}a & b\\ c & d\end{pmatrix}\]
と表したとき、$\det{A}=a- bc \neq 0$ が逆行列の存在条件で、
 \[A^{-1}=\frac{1}{\det{A}}\begin{pmatrix}d & -b\\ -c & a\end{pmatrix}\]
となります。$\det{A} = 0$ のときは逆行列が存在しません。det は determinant の略で行列式ともよばれます。
 
Excel には逆行列を求める関数

=MINVERSE(配列)

が用意されているので、これを用いて A の逆行列などを計算していきます。まず下図で全体のレイアウトを確認してください（前回に入力した行列の右側に追加していきます）。
 

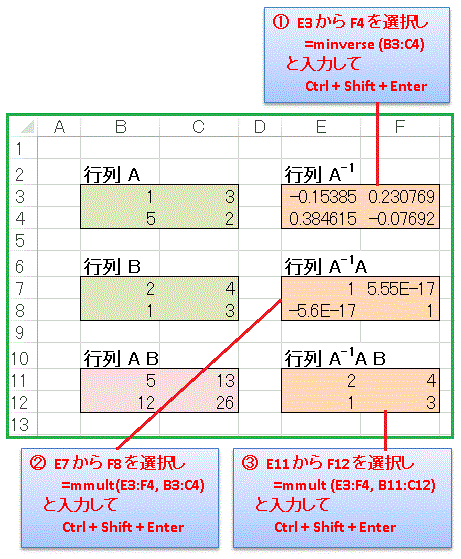
セル E3 から F4 を同時選択状態にして

=MINVERSE(B3:C4)

と入力して Ctrl + Shift + Enter を押して逆行列を出力します。「B3:C4」のところは面倒ならマウスで行列 A の範囲を選択してください。
 
この逆行列 A^-1 が本当に正しいのかどうかを確かめるために、 A に左側から作用させてみましょう。セル E7 から F8 を選択して

=MMULT(E3:F4,B3:C4)

と入れて、[Ctrl] + [Shift] + [Enter] です。引数には逆行列 A^-1 と行列 A の範囲を選択しています。計算結果に少し戸惑うかもしれません。本来なら 0 になるべき成分に 5.55E-17 というような小さな値が残ってしまっています。これは MINVERSE で逆行列を計算するさいに、各成分を detA=ad-bc で割っていることに原因があります。たとえば、数学では 1/3 は「0.3333333 …」のような無限に続く循環小数ですが、コンピューターが計算するときは、どこかで打ち切って近似値として扱うことになります。これは数値計算で割り算するときに、いつもついて回る厄介な現象なのですが、非常に小さな誤差ですから、たとえばベクトルを 1 次変換して座標を求めるぐらいの計算であれば、さほど問題になりません。今のところはあまり気にしないでください。

逆行列を AB に左から作用させれば行列 B に戻ることを確認してみましょう。セル E11 から F12 を選択して

=MMULT(E3:F4,B11:C12)

と入れて、[Ctrl] + [Shift] + [Enter] を押します。引数の範囲はそれぞれ行列 A^-1 と行列 AB に対応する範囲のセルです。計算結果を左にある行列 B と比較して一致していることを確認してください。