曲線の長さ（弧長）

曲線の長さ（弧長）

下図のように区間 $[a,\:b]$ を $n$ 個の小区間に分割します。
 

 
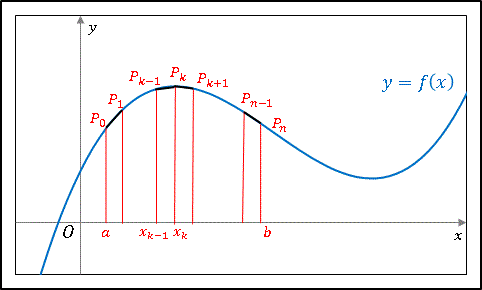
$\Delta x=x_k-x_{k-1}$ が十分に小さければ、弧長 $P_{k-1}P_k$ は線分 $P_{k-1}P_k$ で近似できます。$\Delta y_k=f(x_k)-f(x_{k-1})$ とすれば、
 \[P_{k-1}P_k=\sqrt{(\Delta x_k)^2+(\Delta y_k)^2}=\sqrt{1+\left( \frac{\Delta y_k}{\Delta x_k}\right)^2}\Delta x_k\]
平均値の定理によって、傾き $\Delta y_k/\Delta x_k$ と等しい $f'(c_k)\:(x_{k-1}\lt c_k\lt x_k)$ が存在します。このような小さな線分 $P_{k-1}P_k$ をつなぎ合わせれば曲線 $AB$ の長さを近似できます。さらに分割数を無限にすれば、その極限値は曲線 $AB$ の長さと完全に一致して、
 \[L=\lim_{n\rightarrow \infty}\sum_{k=1}^{n}\sqrt{1+f'(c_k)^2}\Delta x_k=\int_{a}^{b}\sqrt{1+f'(x)^2}dx\]
という積分で与えられることになります。

放物線の弧長

放物線（二次関数）$f(x)=x^2$ の $x=0$ から $x=1$ までの 曲線の長さ（弧長）を求めてみましょう。$f'(x)=2x$ なので
 \[L=\int_{0}^{1}\sqrt{1+4x^2}dx\]
を積分すればよいことになります。そのためには
 \[\int\sqrt{1+a^2x^2}dx=\frac{1}{2a}\left\{ ax\sqrt{1+a^2x^2}+\log (ax+\sqrt{1+a^2x^2})\right\}\]
という公式を使います（こんなものを覚えていられるわけはないので、公式集などから引っ張ってくるのです）。グラフの形から曲線の長さは $\sqrt{2}=1.414$ を少し超えるぐらいだと予測できます。実際に計算してみると
 \[L=\frac{\sqrt{5}}{2}+\frac{1}{4}\log (2+\sqrt{5})=1.4789\]
が得られます。

媒介変数で表された曲線の長さ

曲線の方程式が媒介変数 $t$ を用いて
 \[x=f(t),\quad y=g(t)\]
で与えられている場合、下図のように区間を $n$ 等分します。
 

 
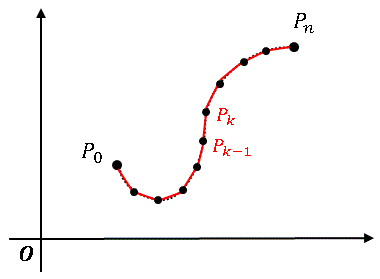
このとき、$P_{k-1}$ と $P_k$ の座標はそれぞれ
 \[P_{k-1}(f(t_{k-1}),\:g(t_{k-1})),\quad P_k(f(t_k),\:g(t_k))\]
で表されるので、線分 $P_{k-1}P_k$ の長さは
 \[P_{k-1}P_k=\sqrt{\{f(t_k)-f(t_{k-1})\}^2+\{g(t_k)-g(t_{k-1})\}^2}\]
で与えられます。平均値の定理より
 \[\begin{align*}f(t_k)-f(t_{k-1})=(t_k-t_{k-1})f'(p_k)\quad (t_{k-1}\lt p_k\lt t_k)\\[6pt]g(t_k)-g(t_{k-1})=(t_k-t_{k-1})g'(q_k)\quad (t_{k-1}\lt q_k\lt t_k)\end{align*}\]
を満たす $p_k,\:q_k$ が存在するので、
 \[P_{k-1}P_k=(t_k-t_{k-1})\sqrt{\{ f'(p_k)\}^2+\{ g'(q_k)\}^2}\]
この小さな線分を全て足し合わせると弧長の近似式となります。
 \[L\simeq\sum_{k=1}^{n}(t_k-t_{k-1})\sqrt{\{ f'(p_k)\}^2+\{ g'(q_k)\}^2}\]
$t$ の動く範囲を $\alpha\leq t\leq \beta$ として、$n\rightarrow \infty$ の極限をとると
\[L=\int_{\alpha}^{\beta}\sqrt{\{ f'(t)\}^2+\{ g'(t)\}^2}dt=\int_{\alpha}^{\beta}\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt\]
という公式が得られます。