アステロイド曲線

アステロイド曲線

アステロイド曲線（asteroid）はギリシア語の「星のような形」に由来する図形で、星芒形あるいは星形ともよばれます。また４つの尖点を持つことから、四尖点形（tetracuspid）の名称でよばれることもあります。アステロイドは、図のように半径 $a$ の大円の内側を半径 $a/4$ の小円が滑ることなく転がるときに、小円の円周上の点が描く軌跡として定義されます。



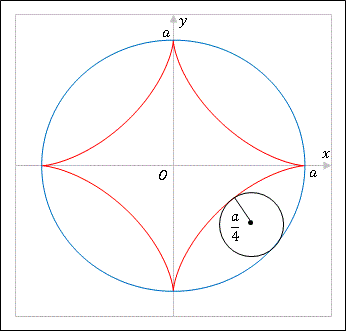
アステロイドの代数曲線は
\[x^{2/3}+y^{2/3}=a^{2/3}\]
によって与えられ、$t$ を媒介変数として
\[x=a\cos^3t,\:\:y=a\sin^3t\quad (a\gt 0)\]
と表すこともできます。媒介変数 $t$ が
\[t\::\:0\quad\longrightarrow\quad\frac{\pi}{2}\quad\longrightarrow\quad\pi\quad\longrightarrow\quad\frac{3}{2}\pi\quad\longrightarrow\quad 2\pi\]
を動くとき $x,\:\:y$ は
\[\begin{align*}&x\::\:a\quad\longrightarrow\quad 0\quad\longrightarrow\quad -a\quad\longrightarrow\quad 0\quad\longrightarrow\quad a\\[6pt]&y\::\:0\quad\longrightarrow\quad a\quad\longrightarrow\quad 0\quad\longrightarrow\quad -a\quad\longrightarrow\quad 0\end{align*}\]
を動いてちょうど一周します。アステロイドはスーパー楕円とよばれる曲線
\[\left|{\frac{x}{a}}\right|^k+\left|{\frac{y}{b}}\right|^k=1\]
において $k=2/3,\:\:a=b$ とおいた形とみることもできます。

アステロイド曲線の面積

アステロイドの媒介変数表示
\[x=a\cos^3t,\:\:y=a\sin^3t\quad (a\gt 0)\]
を用いて曲線に囲まれた内側の面積を計算することができます。第 1 象限の面積を 4 倍すればいいので、
\[S=4\int_{0}^{a}ydx=4\int_{\frac{\pi}{2}}^{0}y\frac{dx}{dt}dt\]
$dx/dt$ を計算すると
\[\frac{dx}{dt}=3a\cos^2t(-\sin t)\]
となるので、
\[\begin{align*}S=&\,12a^2\int_{0}^{\frac{\pi}{2}}\sin^4t\cos^2tdt\\[6pt]=&\,12a^2\int_{0}^{\frac{\pi}{2}}\sin^4t(1-\sin^2t)dt\\[6pt]=&\,12a^2\left(\int_{0}^{\frac{\pi}{2}}\sin^4tdt-\int_{0}^{\frac{\pi}{2}}\sin^6t\right)\end{align*}\]
ここで $\displaystyle a_n=\int_{0}^{\frac{\pi}{2}}\sin^ntdt$ とおくと、漸化式
\[a_0=\frac{\pi}{2},\:\:a_1=1,\:\:a_n=\frac{n-1}{n}a_{n-2}\]
によって定積分を計算できます。$\displaystyle a_6=\frac{5}{6}a_4$ なので、
\[S=12a^2\left(a_4-\frac{5}{6}a_4\right)=2a^2\cdot a_4=2a^2\cdot\frac{3}{4}\cdot\frac{1}{2}\cdot\frac{\pi}{2}=\frac{3}{8}\pi a^2\]
となります。

アステロイド曲線の長さ

$x,\;y$ が媒介変数 $t$ で表されたときの曲線の長さは
\[L=\int_{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt\]
で計算できます。この公式を使ってアステロイド
\[x=a\cos^3t,\:\:y=a\sin^3t\quad (a\gt 0)\]
の１周分の長さを計算してみます。
\[\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2=9a^2\cos^2t\sin^2t\]
となるので、
\[L=4\int_{0}^{\frac{\pi}{2}}3a\cos t\sin tdt=12a\left[\frac{1}{2}\sin^2 t\right]_{0}^{\frac{\pi}{2}}=6a\]
となります。

Excel でアステロイド曲線を描く

　アステロイド曲線は内トロコイド（hypotrochoid） とよばれる曲線群に含まれます。内トロコイドは
\[\begin{align*}x=(r_c-r_m)\cos\theta+r_d\cos\left(\frac{r_c-r_m}{r_m}\theta\right)\\[6pt]
y=(r_c-r_m)\sin\theta-r_d\sin\left(\frac{r_c-r_m}{r_m}\theta\right)\end{align*}\]
で表され、$r_m=r_d,\ r_c=4r_d$ とおいたときに、アステロイド曲線の方程式が得られます。

当サイトからトロコイドを描画するExcelワークシートをダウンロードできます：

≫ ファイルをダウンロードする

ダウンロードしたらファイルを開いて [内トロコイド] のシートを選択してください。
デフォルトでアステロイド曲線が描かれています。



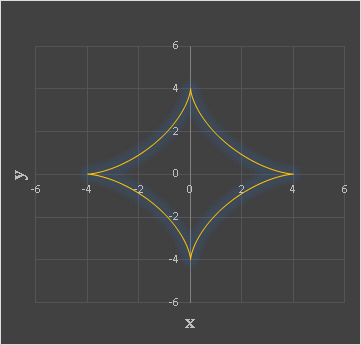
一般に、rm = rd, rc = 4rd に設定したときにアステロイド曲線となります。
たとえば、rc = 2, rm = rd = 0.5 としたときにもアステロイド曲線になります。
rc, rm, rd はスピンボタンで自由に変更できます：



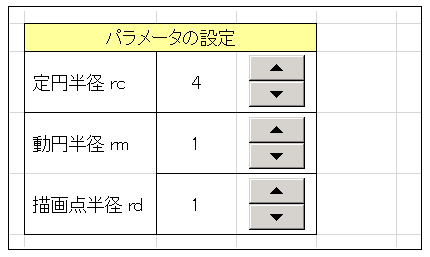
興味のある人はスピンボタンを適当にいじって、アステロイド以外にも色々と試してみてください。たとえば、デフォルト設定から rc を 0.1 下げて 3.9 にするだけでも、アステロイドとは全く異なる曲線が描かれます：

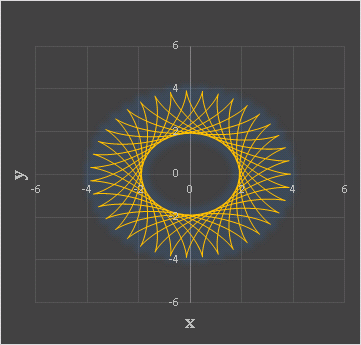
天動説とアステロイド曲線

アステロイド曲線は大昔の天文学において「天動説」を説明するために発見された形です。地球を中心に惑星が回っていると仮定すると「惑星の逆行」という奇妙な動きを説明できません。そこで惑星が小さな円を描きながら地球の周りを動くという「周転円」という考え方で何とかこじつけます。周転円にもとづく天動説は数学的には矛盾がないので、「地動説」支持者にとっては手ごわい理論でした。数学の定理が間違った理論を支えていたこともあるのです。「周転円」の考え方がなければ、人類はもっと早くに「地動説」を受け入れていたかもしれません。