角度の測り方(度数法と弧度法)
図のように、任意の半径の円周上に動点 $P$ をとります。
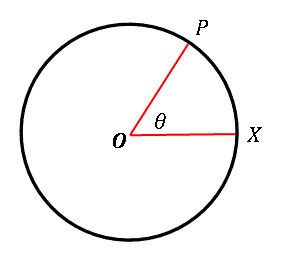
基準線 $OX$ の位置から測った線分 $OP$ の 反時計回りの回転量 $\theta$ を 角度 (angle) と定義します。$OP$ が $1$ 周回って $OX$ に一致したときの回転量を $360^\circ$ であるとします。つまり $1$ 周分の回転量を 360 個の単位(度)に分割します。このような測り方を 度数法 (Degree measure) といいます。$2$ 周すると角度は $720^\circ$ となります。半周ならば $180^\circ$ です。$1/4$ 周のときは
\[\theta=\frac{360^\circ}{4}=90^\circ\]
となり、これは直角と呼ばれます。同様に $1/8$ 周、$1/6$ 周、$1/12$ 周はそれぞれ
\[\begin{align*}\theta=\frac{360^\circ}{8}=45^\circ\\[6pt]\theta=\frac{360^\circ}{6}=60^\circ\\[6pt]\theta=\frac{360^\circ}{12}=30^\circ\end{align*}\]
となります。
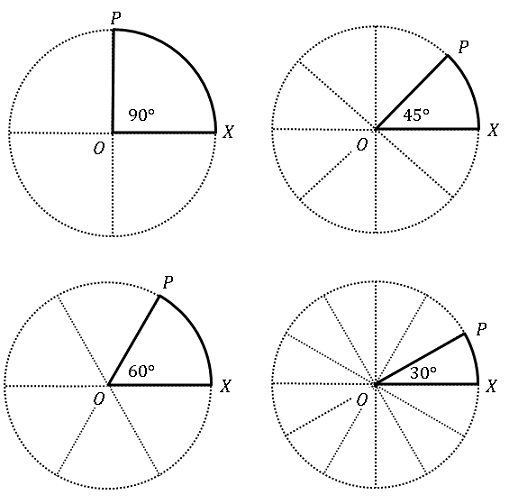
$30^\circ,\:45^\circ,\:60^\circ,\:90^\circ$ は三角形の問題などでよく用いられます。
下図のように単位円(半径 $1$ の円)上の点 $X$ と中心点 $O$ を結ぶ線分を引いて基準線とします(座標系では $x$ 軸に相当します)。
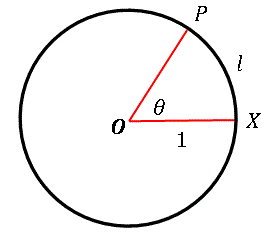
そして任意の円周上の点 $P$ と中心点を結んだ線分 $OP$ が $OX$ となす角度 $\theta$ を 弧 $PX$ の長さ ($=l$) によって定義します ($\theta=l$)。このような角度の測り方を弧度法とよびます。
円周の長さは $2\pi$ となるので、
\[円周の中心角=2\pi\simeq 6.283\]
となります。円を 2 等分すれば半円の中心角は
\[\theta=\frac{2\pi}{2}=\pi\simeq 3.141\]
となり、 四等分したときの扇形の中心角(すなわち直角)は
\[\theta=\frac{2\pi}{4}=\frac{\pi}{2}\simeq 1.571\]
と表せます。一般に円周を $n$ 等分したときの扇形の中心角は
\[\theta=\frac{2\pi}{n}\]
によって表されます。
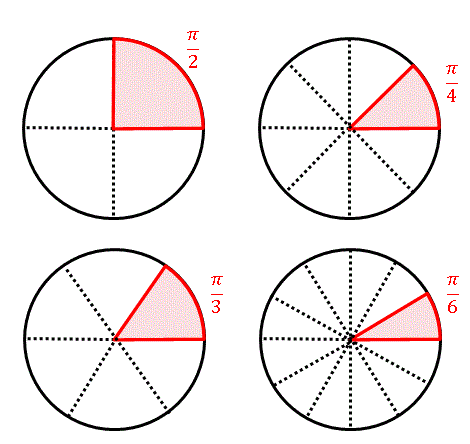
弧度法で表された角度は半円を基準に考えると、大きさのイメージをつかむことができます。たとえば $\theta=\pi/10$ は半円を $10$ 分割しているということです。
弧長 $l=1$ を弧度法における基本単位 ラジアン(radian)と定義します。度数法においては円周の中心角は 360°ですから、ラジアンとの間に
\[2\pi=360^{\circ}\]
の関係があります。つまり
\[\pi=180^{\circ},\quad \frac{\pi}{2}=90^{\circ},\quad\frac{\pi}{3}=60^{\circ},\quad\frac{\pi}{4}=45^{\circ},\quad\frac{\pi}{6}=30^{\circ}\]
というような関係があります。また
\[\begin{align*}&1\:[\mathrm{rad}]=\frac{180}{\pi}^{\circ}=57.2958^{\circ}\\[8pt]&1^{\circ}=\frac{\pi}{180}\:[\mathrm{rad}]=0.017453\:[\mathrm{rad}]\end{align*}\]
というような変換対応になっています。
任意の半径 $r$ の円を考えるとき、円周の長さは半径に比例しますから、角度 $\theta$ の中心角をもつ扇形の弧長は
\[l=r\theta\]
となります。よって半径 $r$ の円の角度を弧度法で測るときは、
\[\theta=\frac{l}{r}\]
と計算できます。三角関数などでは角度に正負の符号をつける場合もあります。点 $OP$ を基準線 $OX$ から反時計回りに測った角度を正、時計回りに測った角度を負と定めています。
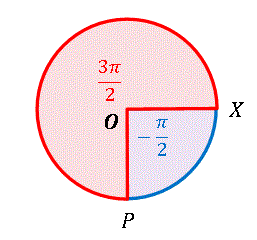
たとえば上図の例では反時計回りに測ると $3\pi/2$ となりますが、時計回りに測ると $-\pi/2$ と表記できます。
$X$ を始点に $P$ が反時計回りに一周したときの角度は $2\pi$ と表記されますが、
\[\theta=2n\pi+\alpha\]
によって $2\pi$ を超える角度を定義することもできます。$n$ は周回番号で、$n=1$ のときは一周すなわち $2\pi,\ n=2$ のときは二周すなわち $4\pi$ を表します。$\alpha$ は $OP$ と $OX$ の位置関係を表す角度です。
【Excel】DEGREES 関数
Excel の DEGREES 関数はラジアンで表された角度を受け取って、度数法の角度に変換します。1ラジアンが度数法で何度なのかを確認してみましょう。セルに
=DEGREES(1)
と入力すると、57.29577951 が返ります。1 ラジアンは 60°弱ぐらいに覚えておくと感覚を掴みやすいです。さきほどの説明の復習も兼ねて、$\pi$ ラジアンが何度になるかを計算してみましょう。円周率の近似値は PI() 関数で得られるので、
=DEGREES(PI())
と入力します。もちろん、戻り値は 180 ですね。$\pi/4$ ラジアンも確認しておきましょう。
=DEGREES(PI()/4)
と入力すると、45 が返ってきます。数値計算上の細かい話をすると、PI() 関数は円周率の 15 桁の近似値に過ぎないので、本来なら DEGREES(PI()) や DEGREES(PI()/4) がきれいな整数値を返すことはなく、若干の誤差を伴うはずです。しかし、Excel は PI() の特定分割値を DEGREES() に渡したときに整数値を返すように内部処理してくれます。
【Excel】RADIANS 関数
Excel の RADIANS 関数は度数法で表された角度を受け取って、ラジアンの角度に変換します。たとえば、
=RADIANS(180)
と入力すると、3.14159265358979 が返ります。これは PI 関数が返す円周率の近似値と同じ値です。実際、
=RADIANS(180)-PI()
と入力すると 0 を返します。同様に、
=RADIANS(90)
は 1.57079632679490 となりますが、これも PI()/2 と同じ値です。

エクセルや数学に関するコメントをお寄せください