余弦積分と正弦積分

この記事では、VBA で余弦積分と正弦積分を実装する方法について解説します。

余弦積分関数Ci(x)

$-\cos t/t$ を $x$ から $\infty$ まで積分するとき、下限値 $x$ を変数とする関数
\[\mathrm{Ci}\,(x)=-\int_{x}^{\infty}\frac{\cos t}{t}dt\tag{1}\]
を余弦積分関数とよびます。余弦積分関数は次のように書けることも知られています。
\[\mathrm{Ci}\,(x)=\gamma+\log x-\int_{0}^{x}\frac{\cos t-1}{t}dt\tag{2}\]
ここで $\gamma$ はオイラーの定数
\[\gamma=\lim_{n\rightarrow \infty}\left(1+\frac{1}{2}+\cdots+\frac{1}{n}-\log n\right)=0.5772156649\tag{3}\]
です。下の図は余弦積分関数 $\mathrm{Ci}\,(x)$ の被積分関数 $f(t)=-\cos t /t$ のグラフです。



余弦積分関数は Excel に用意されていないので、VBA でユーザー定義関数 CI() を作成します。下のコードを標準モジュールに貼り付けて、セルに「=CI(x)」と入力すれば、余弦積分関数 $\mathrm{Ci}\,(x)$ の値を計算して返します。

'[VBA]余弦積分関数

Function CI(x As Double) As Double

　　Dim p As Double, q As Double, r As Double
　　Dim h As Double, s As Double, gm As Double
　　Dim m As Integer, k As Integer

　　gm = 0.5772156649

　　m = 100
　　h = x / (2 * m)

　　s = (Cos(h) - 1) / h + (Cos(2 * h) - 1) / (2 * h)

　　For k = 1 To m - 1
　　　　p = 2 * k * h
　　　　q = (2 * k + 1) * h
　　　　r = (2 * k + 2) * h
　　　　s = s + (Cos(p) - 1) / p + 4 * (Cos(q) - 1) / q + (Cos(r) - 1) / r
　　Next k

　　CI = gm + Log(x) + s * h / 3

End Function

積分アルゴリズムはシンプソンの公式を使っています。CI 関数を使って Excel のワークシートに描いたグラフを載せておきます：

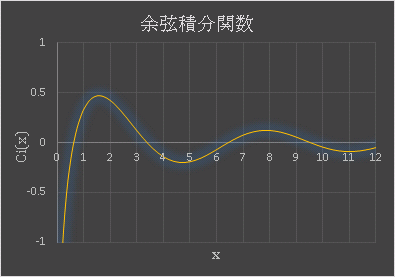
正弦積分関数Si(x)

$\sin t/t$ を $0$ から $x$ まで積分するとき、下限値 $x$ を変数とする積分関数
\[\mathrm{Si}\,(x)=\int_{0}^{x}\frac{\sin t}{t}dt\]
を正弦積分関数とよびます。正弦積分関数の被積分関数は sinc 関数とよばれ、$\mathrm{sinc}(x)$ と表されます。
\[\mathrm{sinc}(x)=\frac{\sin t}{t}\tag{4}\]
sinc 関数の概形は以下のようになります。



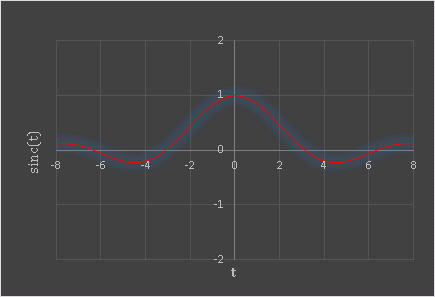
正弦積分関数を計算するユーザー定義関数 SI() のコードも載せておきます。下のコードを標準モジュールに貼り付けてください。ワークシートのセルに「=SI(x)」と入力すれば、正弦積分関数 $\mathrm{Si}\,(x)$ の値を計算して返します。

'[VBA] 正弦積分関数

Function SI(x As Double) As Double

　　Dim p As Double, q As Double, r As Double
　　Dim h As Double, s As Double
　　Dim m As Integer, k As Integer

　　m = 100
　　h = x / (2 * m)

　　s = 1 + Sin(h) / h + Sin(2 * h) / (2 * h)

　　For k = 1 To m - 1
　　　　p = 2 * k * h
　　　　q = (2 * k + 1) * h
　　　　r = (2 * k + 2) * h
　　　　s = s + Sin(p) / p + 4 * Sin(q) / q + Sin(r) / r
　　Next k

　　SI = s * h / 3

End Function

正弦積分関数 SI() をワークシートで使用するときは

=SI(数値)

と入力します。SI関数を使って Excel のワークシートに正弦積分のデータを作成すると、次のようなグラフを描画できます。