【VBA】合流型超幾何関数とラゲール陪多項式

合流型超幾何関数

次の級数で定義される関数をKummer の合流型超幾何関数（Confluent hypergeometric function）といいます。
ERF.PRECISE\[F(a,c\:;x)=1+\frac{a}{c}\frac{x}{1!}+\frac{a(a+1)}{c(c+1)}\frac{x^2}{2!}+\cdots=\sum_{k=0}^{\infty}\frac{(a)_k}{(c)_k}\frac{x^k}{k!}\]
指数関数やエルミート多項式、ベッセル関数などを包括する広いクラスの関数です（たとえば $a=c$ のときに指数関数のマクローリン級数と一致します）。定義式から明らかなように、この関数は $c$ が 0 または負整数のときは分母が 0 となって値をもちません。また、$a$ が負整数であるときには級数は有限項で打ち切られます。たとえば $a=-2$ のときは第 4 項以降はすべて 0 になるので、$F$ は 2 次関数となります。

VBA 数値計算用最新マクロをモジュールに貼り付ける（あるいは上書きする）と、この記事にあるマクロも含めて当サイトに載っている主要な関数を全て利用することができます。ぜひお試しください。

合流型超幾何級数を計算する Function Macro（ユーザー定義関数）です。

'[VBA]合流型超幾何級数
Function CHGEO(a As Double, c As Double, x As Double) As Double
　　Dim d As Double
　　Dim s As Double
　　d = a * x / c
　　s = 1 + d
　　For k = 1 To 200
　　　　d = d * x * (a + k) / (c + k) / (k + 1)
　　　　s = s + d
　　Next k
　　CHGEO = s
End Function

この関数を呼びだすときには、

=CHGEO(a,c,x)

というように記述します。たとえば

=CHGEO(1,1,2)

と入力すると $F(1,1\:;2)=e^2$ を計算して 7.389 という値を返します。

複素変数の合流型超幾何関数

一般には複素変数の合流型超幾何関数が用いられます。
\[F(a,c\:;z)=1+\frac{a}{c}\frac{z}{1!}+\frac{a(a+1)}{c(c+1)}\frac{z^2}{2!}+\cdots=\sum_{k=0}^{\infty}\frac{(a)_k}{(c)_k}\frac{z^k}{k!}\]
複素変数の合流型超幾何関数の実装は次のようになります。

'[VBA]複素変数の合流超幾何関数
Function CXCHGEO(a As Double, c As Double, z As Complex) As Complex
　　Dim d As Double
　　Dim k As Double
　　Dim s As Complex
　　Dim zk As Complex
　　d = a / c
　　s.re = 1 + d * z.re
　　s.im = d * z.im
　　zk = z
　　For k = 2 To 100
　　　　d = d * (a + k - 1) / (c + k - 1) / k
　　　　zk = CPXCLC(zk, z, 3)
　　　　s.re = s.re + d * zk.re
　　　　s.im = s.im + d * zk.im
　　Next k
　　CXCHGEO = s
End Function

変数 z は複素数型 (Complex型) を指定します。CXCHGEO関数を使って、
\[F(1,1,1;i)=\sum_{k=0}^{\infty}(1+i)^k\]
を数値計算してみましょう。

'[VBA](1+i)^kの計算
Sub CXCHGEO_TEST()
　　Dim fz As Complex
　　fz = CXCHGEO(1, 1, CPX(1, 1))
　　Debug.Print fz.re & " + " & fz.im & "i"
End Sub

'1.46869393991589 + 2.28735528717884i

ラゲール陪多項式

合流型超幾何関数には、量子力学において水素原子の波動関数を記述するときに用いられるラゲール陪多項式が含まれています。ラゲール陪多項式は母関数によって
\[g(t,x)=\frac{(-1)^k}{(1-t)^{k+1}}\exp\left(-\frac{xt}{1-t}\right)=\sum_{n=k}^{\infty}L_n^k(x)\frac{t^{n-k}}{n!}\]
と定義されています。つまり $g(t,x)$ を級数展開したときの $t^{n-k}/n!$ の係数が $L_n^k(x)$ です。合流型超幾何関数を用いると
\[L_n^k(x)=(-1)^k\frac{(n!)^2}{k!(n-k)!}F(k-n,k+1\:;x)\]
と表されます。特に $k=0$ のときには ラゲール多項式 とよばれ、$L_n^0(x)$ の添え字 0 を省略して単に $L_n(x)$ と書くこともあります。ラゲール陪多項式 $L_n^k(x)$ はラゲール多項式の $k$ 階微分という関係になっています。
\[L_n^k(x)=\frac{d^k}{dx^k}L_n(x)\]
$L_n(x)$ を具体的に書き下してみると
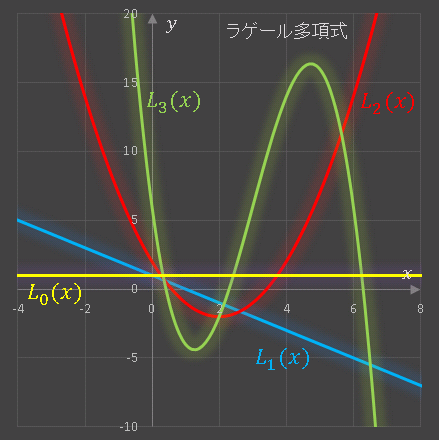
\[\begin{align*}L_0(x)&=1\\[6pt]L_1(x)&=-x+1\\[6pt]L_2(x)&=x^2-4x+2\\[6pt]L_3(x)&=-x^3+9x^2-18x+6\end{align*}\]
それぞれ微分すると $L_n^1(x)$ が得られます。
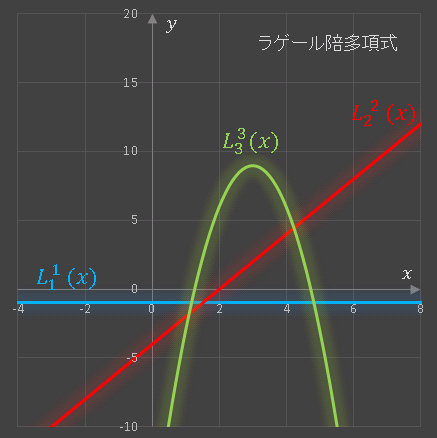
\[\begin{align*}L_1^1(x)&=-1\\[6pt]L_2^1(x)&=2x-4\\[6pt]L_3^1(x)&=-3x^2+18x-18\end{align*}\]
これをさらに繰り返し微分していくと、ラゲール陪多項式 $L_n^k(x)$ の系列が得られます。

ラゲール陪多項式のマクロ

ラゲール陪多項式を計算するマクロは以下のようになります。

'[VBA]ラゲール陪多項式
Function LAG(n As Integer, k As Integer, x As Double)
　　nfact = WorksheetFunction.fact(n)
　　kfact = WorksheetFunction.fact(k)
　　nkfact = WorksheetFunction.fact(n - k)
　　LAG = (-1) ^ k * nfact ^ 2 * CHGEO(k - n, k + 1, x) / kfact / nkfact
End Function

このユーザー定義関数は

=LAG(n,k,x)

の形で呼びだします。たとえば

=LAG(2,1,3)

と入力すると $L_2^1(3)$ を計算します。LAG 関数を使ってワークシートにラゲール多項式 $L_n(x)$ のグラフを描くと次のようになります。



$L_n(x)$ の導関数である $L_n^1(x)$ のグラフは次のようになります。