【VBA】ニュートン・ラフソン法

この記事では VBA でニュートン・ラフソン法で方程式の数値解を求めるプログラムを実装する方法について解説します。

【VBA】ニュートン・ラフソン法

高次方程式 $f(x)=0$ の近似解を求めるときにはニュートン・ラフソン法 (Newton-Raphson method) がよく用いられます。

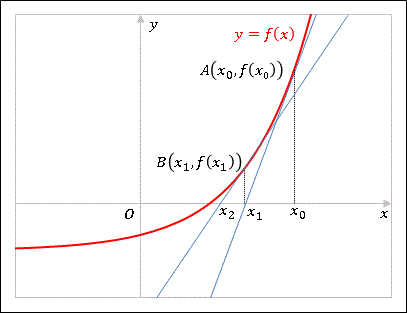
上の図のように適当な初期値 $x_0$ を与えます。このとき $A(x_0,f(x_0))$ に接線を引いて、$x$ 軸と交わる点を $x_1$ とします。すると $A$ 点における接線の勾配は
\[f'(x_0)=\frac{f(x_0)}{x_0-x_1}\]
と表すことができます。これを変形すると
\[x_1=x_0-\frac{f(x_0)}{f'(x_0)}\]
というように $x$ 軸との交点の座標が求まります。今度は $B(x_1,f(x_1))$ に接線を引いて $x$ 軸と交わる点を $x_2$ とすると、$x$ 軸との交点の座標は
\[x_2=x_1-\frac{f(x_1)}{f'(x_1)}\]
で与えられます。これを繰り返すと交点は $f(x)=0$ の解に近づいていきます。一般に $n+1$ 回目の解は
\[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\]
で表されますが、$|x_{n+1}-x_n|$ があらかじめ定めた収束判定定数 EPS より小さくなったところで計算を打ち切り、そのときの $x_{n+1}$ を方程式の近似解とします。

$x^2-2x-3=0$ の近似解をニュートン・ラフソン法で計算するプロシージャです。

'[VBA] ニュートン・ラフソン法 (Newton-Raphson method)

Sub Newton_Raphson()

　　Dim eps As Double
　　Dim x0 As Double
　　Dim xn As Double
　　Dim k As Integer

　　'初期値
　　x0 = InputBox("初期値を入力してください")

　　'収束判定定数
　　eps = 0.001

　　'|sn-s0|が eps より大きい間は処理を繰り返します
　　Do While Abs(xn - x0) > eps And k < 100
　　　　k = k + 1
　　　　xn = x0
　　　　x0 = xn - (xn ^ 2 - 2 * xn - 3) / (2 * xn - 2)
　　Loop

　　If k < 100 Then
　　　　MsgBox xn
　　Else
　　　　MsgBox "解はみつかりませんでした"
　　End If

End Sub

Newton_Raphson() を実行すると初期値の入力が促されるので「 5 」を入れてみると

3.00060975609756

という近似解が表示されます（真の解は $x=3$）。初期値を「-5」とすると、もう 1 つの解

-1.00006103608759

が得られます。eps の値を小さくするほど精度が上がります。

Do While Abs(xn - x0) > eps And k < 100

の “And k < 100” は安全装置で、ループの中でカウント数 k を 1 つずつ増やして k が 100 になっても解がみつからない場合は繰り返し処理を停止させます（無限ループを回避します）。試しに

x0 = xn - (xn ^ 2 - 2 * xn - 3) / (2 * xn - 2)

の部分を

x0 = xn - (xn ^ 2 + 1) / (2 * xn)

に変えて実行してみてください。これは $x^2+1=0$ の解を求めさせようとするものですが、当然実数範囲に解はないので処理を途中でやめて「解はみつかりませんでした」というメッセージが表示されます。