正三角形の性質（角度・面積・周長・対称性）

正三角形の基本

正三角形 (equilateral triangle)は三辺の長さが全て等しい三角形です。



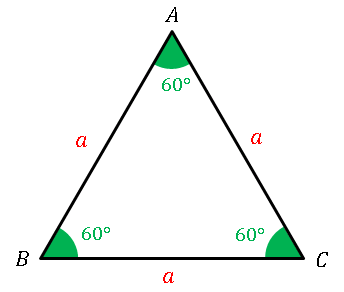
内角も全て等しく、
\[\angle ABC=\angle BCA=\angle CAB=60^{\circ}=\frac{\pi}{3}\]
となっています。周の長さは $3a$ です。

正三角形の面積

辺の長さが有理数（分数で表せる数）であれば、点 $A$ から 辺 $BC$ に下ろした垂線の長さ（すなわち正三角形の高さ）$AH$ は必ず無理数となります。



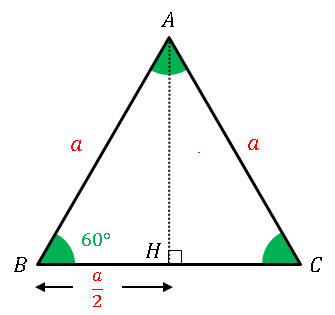
これは次のようにしてわかります。
図において $\triangle ABH$ に三平方の定理（ピタゴラスの定理）を用いると
\[AB^2=AH^2+BH^2\]
が成り立つので
\[AH=\sqrt{AB^2-AH^2}=\sqrt{a^2-\left(\frac{a}{2}\right)^2}=\frac{\sqrt{3}a}{2}\simeq 0.866a\]
となります。有理数と無理数の積は有理数となるので、正三角形の高さは無理数になります。



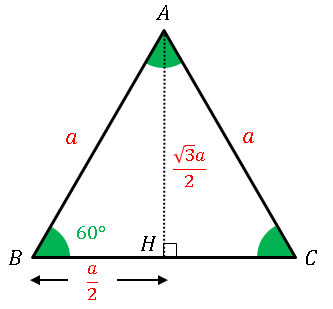
逆に高さが有理数 $b$であったとすると、
\[BH:AB:AH=1:2:\sqrt{3}=\frac{b}{\sqrt{3}}:\frac{2b}{\sqrt{3}}:b\]
という比例関係により辺の長さは無理数となります。また、各辺の長さが $a$ である正三角形の面積は
\[S=\frac{1}{2}AB\cdot BC\]
を計算して
\[S=\frac{\sqrt{3}a^2}{4}\simeq 0.433a^2\]
で与えられます。

正三角形の対称性

正三角形の各頂点から垂線を下ろし、その垂線に対して折り重ねることができます（垂線が対称軸となっています）。また、各垂線が交わる点 $O$ は正三角形の重心と一致します。



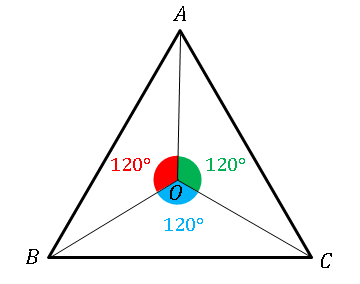
図のように $AO,\,BO,\,CO$ は中心角を 3 等分します：
\[\angle AOB=\angle BOC=\angle COA=120^{\circ}=\frac{2\pi}{3}\]
すなわち、正三角形はその重心を中心に $120^{\circ}$ の回転対称軸をもちます ($120^{\circ}$ 回転させると重なります)。